Первое начало термодинамики, термохимия

Изолированные, открытые и закрытые системы, классический и статистический подходы к описанию термодинамических систем. Интенсивные и экстенсивные параметры состояния системы. Теплота. Работа. Внутренняя энергия. Первое начало термодинамики. Уравнения состояния. Функции состояния. Закон Гесса. Стандартные состояния.

Энтропия. Второе и третье начала термодинамики

Состояние системы и микросостояния системы, степень вырождения, допустимые микросостояния. Эргодическая гипотеза. Энтропия. Температура. Связь внутренней энергии, энтропии и температуры. Теплоемкость. Свойства энтропии. Второе начало термодинамики. Обратимые и необратимые процессы. Третье начало термодинамики.

Термодинамические потенциалы

Характеристические функции. Термодинамические потенциалы - внутренняя энергия, энтальпия, потенциал Гельмгольца, потенциал Гиббса. Фундаментальные уравнения и термодинамические соотношения между термодинамическими величинами. Уравнения Максвелла. Уравнение Гиббса  -  Гельмгольца. (Необходимый математический аппарат -  Якобиан. Алгебраические соотношения для детерминантов матриц Якоби второго ранга.)

1. (1/1-99). Какие из перечисленных ниже функций являются функциями состояния, а какие - термодинамическими потенциалами?

Н + PV, H 2 +5PV MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGibaabaGaaGOmaaaacqGHRaWkcaaI1aGaamiuaiaadAfaaaa@3AD7@ , G S +10TS MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGhbaabaGaam4uaaaacqGHRaWkcaaIXaGaaGimaiaadsfacaWGtbaaaa@3BA9@ , A + PV , A PV + T V S MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGbbaabaGaamiuaiaadAfaaaGaey4kaSYaaSaaaeaacaWGubaabaGaamOvaaaacaWGtbaaaa@3BF1@ .

Почему? Напишите фундаментальные уравнения для термодинамических потенциалов.

2. (1/Э-96), (1/Э-98). Вывести выражение для изобарно-изотермического потенциала через термодинамические параметры и параметры статистической физики.

3. (1/Э-01). Вывести выражения для термодинамического потенциала Гиббса через термодинамические параметры и параметры статистической термодинамики. Какими свойствами обладает потенциал Гиббса и когда его используют?

4. (1/Э-97). Вывести выражения для изохорно-изотермического потенциала через термодинамические параметры и через параметры статистической физики.

5. (1/Э-00). Вывести соотношения Гиббса  -  Гельмгольца. В каких случаях используют эти соотношения?

6. (1/Э-02). Вывести выражения для термодинамического потенциала Гельмгольца, внутренней энергии и энтропии через параметры статистической термодинамики. Какими свойствами обладает потенциал Гельмгольца и когда его используют?

7. (1/1-95). Показать, что адиабатическое расширение идеального газа всегда сопровождается его охлаждением.

8. (2/1-96). Доказать, что при адиабатическом процессе внутренняя энергия системы является возрастающей функцией температуры.

9. (5/1-96). Термическое и калорическое уравнения состояния идеального электронного газа связаны соотношением PV = 2/3 U. Найти для этого газа уравнение адиабаты в переменных P - V.

10. (1/Э-06).* Известно термическое уравнение состояния газа Ван-дер-Ваальса: (P+ a V 2 )(V−b)=RT. MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaiikaiaadcfacqGHRaWkdaWcaaqaaiaadggaaeaacaWGwbWaaWbaaSqabeaacaaIYaaaaaaakiaacMcacaGGOaGaamOvaiabgkHiTiaadkgacaGGPaGaeyypa0JaamOuaiaadsfacaGGUaaaaa@4331@ Выведите калорическое уравнение состояния газа Ван-дер-Ваальса U = U (T,V)
Решение

11. (1/1-98). Для газа, подчиняющегося уравнению Ван-дер-Ваальса P= RT V−b − a V 2 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiuaiabg2da9maalaaabaGaamOuaiaadsfaaeaacaWGwbGaeyOeI0IaamOyaaaacqGHsisldaWcaaqaaiaadggaaeaacaWGwbWaaWbaaSqabeaacaaIYaaaaaaaaaa@3FDE@ , справедливо соотношение ( ∂P ∂T ) v = R V−b MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadcfaaeaacqGHciITcaWGubaaaaGaayjkaiaawMcaamaaBaaaleaacaWG2baabeaakiabg2da9maalaaabaGaamOuaaqaaiaadAfacqGHsislcaWGIbaaaaaa@41CD@ .

Найдите для этого газа значения  ( ∂U ∂V ) T , ( ∂ c V ∂V ) T ,  ( ∂T ∂V ) U ,  ( ∂T ∂V ) S MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadwfaaeaacqGHciITcaWGwbaaaaGaayjkaiaawMcaamaaBaaaleaacaWGubaabeaakiaacYcadaqadaqaamaalaaabaGaeyOaIyRaam4yamaaBaaaleaacaWGwbaabeaaaOqaaiabgkGi2kaadAfaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadsfaaeqaaOGaaiilaiaaykW7daqadaqaamaalaaabaGaeyOaIyRaamivaaqaaiabgkGi2kaadAfaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadwfaaeqaaOGaaiilaiaaykW7daqadaqaamaalaaabaGaeyOaIyRaamivaaqaaiabgkGi2kaadAfaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadofaaeqaaaaa@58CA@ .

Получите калорическое уравнения состояния газа Ван-дер-Ваальса, используя полученные соотношения.

12. (1/1-02). Найти ( ∂T ∂V ) U MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadsfaaeaacqGHciITcaWGwbaaaaGaayjkaiaawMcaamaaBaaaleaacaWGvbaabeaaaaa@3D0C@ и ( ∂T ∂V ) S MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadsfaaeaacqGHciITcaWGwbaaaaGaayjkaiaawMcaamaaBaaaleaacaWGtbaabeaaaaa@3D0A@ для газа Ван -дер-Ваальса с уравнением состояния ( P+ a V 2 )( V−b )=RT MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacaWGqbGaey4kaSYaaSaaaeaacaWGHbaabaGaamOvamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaadaqadaqaaiaadAfacqGHsislcaWGIbaacaGLOaGaayzkaaGaeyypa0JaamOuaiaadsfaaaa@42DF@ и известной теплоемкостью С _V. Дать качественное пояснение особенности рассматриваемых процессов.

13. (3/Э1-94,99). В вакуумированном объеме с адиабатической оболочкой приводят в соприкосновение два твердых образца одного вещества. Начальные температуры образцов различаются. Приняв количества вещества в образцах одинаковыми и теплоемкость вещества постоянной, определите изменение энтропии при переходе системы к термическому равновесию. Как изменится ответ, если в объеме исходно находился также воздух?

14. (2/1-02). Система состоит из двух теплоизолированных колб, разделенных теплонепроницаемой перегородкой. Исходно в каждой из колб находится по одному молю одного и того же идеального газа при одинаковом давлении р, но разной температуре: Т₁ и Т₂. Найти изменение энтропии этой системы при удалении перегородки и достижении состояния термодинамического равновесия, если с _v этого газа не зависит от температуры.

15. (2/1-05). Определите отношение W ΔS MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGxbaabaGaeuiLdqKaam4uaaaaaaa@3917@ , где W - работа, затрачиваемая на изотермическое сжатие одного моля идеального газа при T = 450 K от объема V ₁ = 45 л до объема V₂ = 24 л Δ S - - изменение энтропии газа в указанном процессе.

16. (1/Э-05).* Углекислый газ подчиняется уравнению состояния Ван-дер-Ваальса ( P+ a V 2 )( V−b )=RT MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaacaWGqbGaey4kaSYaaSaaaeaacaWGHbaabaGaamOvamaaCaaaleqabaGaaGOmaaaaaaaakiaawIcacaGLPaaadaqadaqaaiaadAfacqGHsislcaWGIbaacaGLOaGaayzkaaGaeyypa0JaamOuaiaadsfaaaa@42DF@ с параметрами α= 0,364 Дж·м^3.моль^-2 и b = 4,27· 10 ^{- 5} м³/моль. Оцените изменение внутренней энергии в процессе сжатия одного моля CO₂ с объема V ₁ = 10 л до V ₂ = 1 л, проводимом при 298 К.
Решение

17. (2/1-06).* Доказать соотношение: ( ∂T ∂V ) U = P− ( ∂P ∂T ) V T C V MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadsfaaeaacqGHciITcaWGwbaaaaGaayjkaiaawMcaamaaBaaaleaacaWGvbaabeaakiabg2da9maalaaabaGaamiuaiabgkHiTmaabmaabaWaaSaaaeaacqGHciITcaWGqbaabaGaeyOaIyRaamivaaaaaiaawIcacaGLPaaadaWgaaWcbaGaamOvaaqabaGccaWGubaabaGaam4qamaaBaaaleaacaWGwbaabeaaaaaaaa@49BA@ . Как будет изменяться при адиабатическом расширении в вакуум температура неидеального газа c фактором сжимаемости PV RT ≡Z(V,T) MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGqbGaamOvaaqaaiaadkfacaWGubaaaiabggMi6kaadQfacaGGOaGaamOvaiaacYcacaWGubGaaiykaaaa@3FC2@ ?
Решение

18. (2/1-99). Уравнение состояния моля реального газа описывается соотношением P = RT/(V - b) - a/V² c a > 0, b > 0 Как изменится температура этого газа при необратимом адиабатическом расширении газа в вакуум?

19. (1/Э-95). Найти выражение для разности теплоемкостей c _р и c _v в виде, удобном для вычисления в случае произвольной системы через функции ее состояния. Проверить правильность найденного выражения для ситуации идеального газа.

20. (1/1-01).
Докажите справедливость соотношения c p − c ν =T ( ∂P ∂T ) V ( ∂V ∂T ) P MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaakiabgkHiTiaadogadaWgaaWcbaGaeqyVd4gabeaakiabg2da9iaadsfadaqadaqaamaalaaabaGaeyOaIyRaamiuaaqaaiabgkGi2kaadsfaaaaacaGLOaGaayzkaaWaa0baaSqaaiaadAfaaeaaaaGcdaqadaqaamaalaaabaGaeyOaIyRaamOvaaqaaiabgkGi2kaadsfaaaaacaGLOaGaayzkaaWaa0baaSqaaiaadcfaaeaaaaaaaa@4BE2@ .

21. (4/1-99).
Докажите справедливость соотношения c p − c ν =−T ( ∂P ∂T ) V 2 ( ∂V ∂P ) T MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaakiabgkHiTiaadogadaWgaaWcbaGaeqyVd4gabeaakiabg2da9iabgkHiTiaadsfadaqadaqaamaalaaabaGaeyOaIyRaamiuaaqaaiabgkGi2kaadsfaaaaacaGLOaGaayzkaaWaa0baaSqaaiaadAfaaeaacaaIYaaaaOWaaeWaaeaadaWcaaqaaiabgkGi2kaadAfaaeaacqGHciITcaWGqbaaaaGaayjkaiaawMcaamaaDaaaleaacaWGubaabaaaaaaa@4D8B@

22. (3/1-00).
Докажите справедливость соотношения ( ∂ c P ∂V ) T 2 =−T ( ∂ 2 V ∂ T 2 ) P ( ∂P ∂V ) T MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadogadaWgaaWcbaGaamiuaaqabaaakeaacqGHciITcaWGwbaaaaGaayjkaiaawMcaamaaDaaaleaacaWGubaabaGaaGOmaaaakiabg2da9iabgkHiTiaadsfadaqadaqaamaalaaabaGaeyOaIy7aaWbaaSqabeaacaaIYaaaaOGaamOvaaqaaiabgkGi2kaadsfadaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaWaa0baaSqaaiaadcfaaeaaaaGcdaqadaqaamaalaaabaGaeyOaIyRaamiuaaqaaiabgkGi2kaadAfaaaaacaGLOaGaayzkaaWaa0baaSqaaiaadsfaaeaaaaaaaa@51DE@ .

23. (1/1-03). Показать, что c p − c V =−T[ ( ∂ 2 G ∂ T 2 ) p − ( ∂ 2 A ∂ T 2 ) V ] MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaakiabgkHiTiaadogadaWgaaWcbaGaamOvaaqabaGccqGH9aqpcqGHsislcaWGubWaamWaaeaadaqadaqaamaalaaabaGaeyOaIy7aaWbaaSqabeaacaaIYaaaaOGaam4raaqaaiabgkGi2kaadsfadaahaaWcbeqaaiaaikdaaaaaaaGccaGLOaGaayzkaaWaaSbaaSqaaiaadchaaeqaaOGaeyOeI0YaaeWaaeaadaWcaaqaaiabgkGi2oaaCaaaleqabaGaaGOmaaaakiaadgeaaeaacqGHciITcaWGubWaaWbaaSqabeaacaaIYaaaaaaaaOGaayjkaiaawMcaamaaBaaaleaacaWGwbaabeaaaOGaay5waiaaw2faaaaa@52A7@ .

24. (2/1-04).* Показать,  что c p − c V =−T ∂ 2 G ∂T∂P ∂ 2 A ∂T∂V MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaakiabgkHiTiaadogadaWgaaWcbaGaamOvaaqabaGccqGH9aqpcqGHsislcaWGubWaaSaaaeaacqGHciITdaahaaWcbeqaaiaaikdaaaGccaWGhbaabaGaeyOaIyRaamivaiabgkGi2kaadcfaaaWaaSaaaeaacqGHciITdaahaaWcbeqaaiaaikdaaaGccaWGbbaabaGaeyOaIyRaamivaiabgkGi2kaadAfaaaaaaa@4D10@ .
Решение

25. (1/1-94). Для неидеального газа, подчиняющегося уравнению состояния

p V ¯ =RT+BP+APT, MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaanaaabaGaamOvaaaacqGH9aqpcaWGsbGaamivaiabgUcaRiaadkeacaWGqbGaey4kaSIaamyqaiaadcfacaWGubGaaiilaaaa@4108@

где V ¯ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa0aaaeaacaWGwbaaaaaa@36D9@ - мольный объем, А и В - характеристические постоянные газа. Найдите значение c p − c ν MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaakiabgkHiTiaadogadaWgaaWcbaGaeqyVd4gabeaaaaa@3BB9@ .

26. (2/Э-02). Мольный объем газа описывается уравнением состояния

V ¯ = RT P + βT P 2 +γPT MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaa0aaaeaacaWGwbaaaiabg2da9maalaaabaGaamOuaiaadsfaaeaacaWGqbaaaiabgUcaRmaalaaabaGaeqOSdiMaamivaaqaaiaadcfadaahaaWcbeqaaiaaikdaaaaaaOGaey4kaSIaeq4SdCMaamiuaiaadsfaaaa@43DF@

где β = 1,42⁴ м³Па²/K и γ = 2,43 ·10 ^{- 11} м³/(Па*K). Этот газ, находящийся изначально при давлении 1 бар, нагревают от температуры 298 K до температуры 318  К и затем сжимают до давления 48 бар. Определите изменение энтальпии для одного моля газа, если известно, что в указанном температурном интервале изобарная мольная теплоемкость газа практически постоянна и равна 31,56 Дж/моль К.

27. (1/1-06).* Обратимые процессы, в ходе которых теплоемкость системы C остаётся постоянной, называют политропными. Найдите зависимость Р( V , T) для политропного процесса (уравнение политропы) для идеального газа. Какие политропные процессы вам известны?
Решение

28. (1/1-00). Реальный газ описывается уравнением состояния p V ¯ =RT+aP+bPT MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiCamaanaaabaGaamOvaaaacqGH9aqpcaWGsbGaamivaiabgUcaRiaadggacaWGqbGaey4kaSIaamOyaiaadcfacaWGubaaaa@4098@ с константами α =  2,6 ·10 ^{- 4} м³/моль и β = 1,12· 10 ^{- 6} м³/(моль· К). Три моля этого газа изотермически (Т = 310 К) расширяются от объема V₁ = 30 л до объема V₂ = 72 л. Рассчитайте изменение молярной теплоемкости с _P в этом процессе.

29. (3/1-04). Для 1 моля газа, описанного в предыдущей задаче (1/1-00), рассчитать изменение энтальпии при сжатии от давления 1 атм, 273 К до давления 50 атм и температуры 318 К. Значение стандартной изобарной теплоемкости для этого газа с_Р⁰ составляет 28,8 Дж/(моль*К) и слабо зависит от температуры в указанном диапазоне температур.

30. (1/1-97). Реальный газ описывается уравнением состояния P   =   RT/V +  α /V² с константой α = 1,6 ·10 ^{- 2} Па м⁶. Два моля этого газа изотермически расширяются от объема V₁ = 24 л до объема V₂ = 48 л при температуре 300 К. Определите изменение молярной теплоемкости c_V в указанном процессе.

31. (1/1-07). Для газа Дюпре, подчиняющегося уравнению состояния P( V - b) =RT, вычислите значения коэффициента Джоуля  -  Томпсона
μ _JT= ( ∂T ∂P ) H MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaeWaaeaadaWcaaqaaiabgkGi2kaadsfaaeaacqGHciITcaWGqbaaaaGaayjkaiaawMcaamaaBaaaleaacaWGibaabeaaaaa@3CF9@ при давлении 3 ·10⁴ Па и температуре 350 K. В указанной точке c_P = 24 Дж/(моль^.К). Величина b постоянна и равна 4,8·10 ^{- 4} м³.

32. (1/Э-04).* Распространение звука в идеальном газе можно рассматривать как адиабатический процесс. Из гидродинамики

известно, что скорость звука с ={(∂P/∂ρ)_адиаб}^0,5,, где P – давление, а ρ плотность газа. Найти скорость звука в гелии при комнатной температуре, если теплоемкость одноатомного идеального газа С_v = 3/2 R, атомный вес М _Не = 4.
Решение

33. (1/1-08). Студент-химик поет песню, вдохнув вместо воздуха гелий. Определите, как изменилась частота звука. Известно, что скорость звука в газе определяется соотношением

υ= V α⋅M MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbqaq=labew8a1jabg2da9maakaaabaWaaSaaaeaacaWGwbaabaGaeqySdeMaeyyXICTaamytaaaaaSqabaaaaa@3FBE@ , где α=− 1 V ⋅ ( ∂V ∂P ) S MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqySdeMaeyypa0JaeyOeI0YaaSaaaeaacaaIXaaabaGaamOvaaaacqGHflY1daqadaqaamaalaaabaGaeyOaIyRaamOvaaqaaiabgkGi2kaadcfaaaaacaGLOaGaayzkaaWaaSbaaSqaaiaadofaaeqaaaaa@4488@ , V – мольный объем газа, М – молярная масса газа. Изобарные теплоемкости воздуха и гелия равны 29,15 и 20,78 Дж/(моль ·К), соответственно. Газы считать идеальными.

34. (5/1-01). Найти температуру, при которой у жидкой воды теплоемкости при постоянном давлении и постоянном объеме одинаковы, если известно, что зависимость мольного объема воды от температуры дается выражением:

V (см³) = 18,0011 – 0,00084 t + 0,00012 t²( 0 °C < t < 20 °C).

35. (5/1-94). В дьюаровский сосуд, содержащий 5 кг воды при температуре 303 К, внесли 1 кг снега при 263 К. Найдите изменение энтропии этой системы после установления термодинамического равновесия.

ΔH_{пл.снPснPв}= 4,2 кДж/(кг ·×К).

36. (2/1-01). Энтальпия фазового перехода между двумя кристаллическими модификациями описывается выражением

справедливым от 0 К до температуры фазового перехода. Найти температуру фазового перехода.

37. (2/1-98).* Вычислить изменение потенциала Гиббса в процессе затвердевания 1 кг переохлажденного бензола при 268,2 К. Давление насыщенного пара твердого бензола при 268,2 К 2279,8 Па, а над жидким бензолом при этой же температуре – 2639,7 Па. Вывести формулы для расчета. Пары бензола считать идеальным газом.
Решение

38. (2/1-03). При 298  К и давлении 0,1013  МПа абсолютные энтропии ромбической серы и моноклинной серы равны 31,88 и 32,55 Дж (моль·К). Теплоты сгорания ромбической и моноклинной серы соответственно равны –296,9 и –297,2 кДж/ моль. Найти значение ΔG⁰ для процесса превращения серы ромбической в серу моноклинную при 298  К. Какая модификация серы при этих условиях более устойчива?

39.(3/1-01). Рассчитать изменение энтропии при адиабатическом смешении 1 моля Не, в зятого при 293 К и давлении 1 бар, с 2 молями О₂, находящегося при 323 К и давлении 1 бар. Давление результирующей смеси 1 бар. Известно, что С_{P Не} =5/2 R, С _PО2 = 7/2 R.

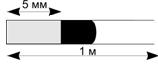40.(6/1-03). В закрытой с одного конца металлической трубке диаметром d = 7,62 мм и длиной 1  м в 5 мм от закрытого конца находится свинцовый грузик массой m =  9 г. В пространстве между грузиком и замкнутым концом находится 0,1 моль газа под давлением 10⁴  атм и с температурой 300 К. Газ начинает адиабатически расширяться, выталкивает грузик из трубки и дальше расширяется в атмосферу. Найти температуру выходящих из трубки газов и полную совершенную газом работу. Какая часть из этой работы приходится на выталкивание грузика из трубки? Газ считать идеальным с с _V  = 16,62  Дж/  (моль ·К).

41. (4/1-96). Известно, что в термодинамических справочниках стандартные значения термодинамических функций Δ f H 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadAgaaeqaaOGaamisamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3CA3@ и S 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3A27@ для газообразных веществ даны для стандартного давления газа 1 бар. В некоторых теоретических расчетах вместо давления обычно используют концентрации газа, выраженные в числе частиц на 1 см³ объема; при этом за стандартные значения Δ f H 298 o ′ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadAgaaeqaaOGaamisamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaaceWGVbGbauaaaaaaaa@3CAF@ и S 298 o ′ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaaceWGVbGbauaaaaaaaa@3A33@ kfsin20.files/image002 принимают значения этих термодинамических функций при концентрации 1 частица в 1 см³. Найти, как соотносятся величины Δ f H 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadAgaaeqaaOGaamisamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3CA3@ и Δ f H 298 o ′ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadAgaaeqaaOGaamisamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaaceWGVbGbauaaaaaaaa@3CAF@ , а также S 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3A27@ и S 298 o ′ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4uamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaaceWGVbGbauaaaaaaaa@3A33@ для идеальных газов.

42. (5/1-95). Согласуются ли приведенные в таблице величины (в единицах ккал/моль) друг с другом? Рассчитать из приведенных данных теплоту атомизации твердых оксидов. Полагать D O 2 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiramaaDaaaleaacaWGpbWaaSbaaWqaaiaaikdaaeqaaaWcbaGaam4Baaaaaaa@399F@ = 118 ккал/моль.

43. (2/1-08). Найти абсолютную стандартную энтропию твердого аммиака при Т = 15 К, если известно, что при этой температуре c p MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaaaaa@37F6@ = 0,84 Дж/(моль ·К), а в диапазоне температур 0 ÷25 К теплоемкость описывается формулой Дебая: c p =a⋅ T 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4yamaaBaaaleaacaWGWbaabeaakiabg2da9iaadggacqGHflY1caWGubWaaWbaaSqabeaacaaIZaaaaaaa@3DF9@ .

44. (1/1-96). Определить теплоту образования Δ f H 298 o MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadAgaaeqaaOGaamisamaaDaaaleaacaaIYaGaaGyoaiaaiIdaaeaacaWGVbaaaaaa@3CA3@ газообразных атомов фосфора, если известны теплоты следующих реакций:

45. (3/1-06).* Оценить величину энергии связи в молекуле О₂, если известно, что изобарный тепловой эффект каталитической реакции окисления орто-ксилола до фталевой кислоты, записываемой уравнением

о-С₈Н_10(ж.) + 6О_(г.) = С₈Н₆О_4(кр.) + 2Н₂О_(ж.),

равен –2824,49 кДж/моль. Теплота сгорания фталевой кислоты равна 3223,33 кДж/моль.