110. (1/2-00). Зависимость температуры плавления Sn от давления (в бар) передается выражением: t(°С) = 231,8 + 0,0032(P–1).
Найти плотность твердого олова r _тв, учитывая, что Q_пл = 7,2 кДж/моль и r _ж = 6,988 г/см³.
Молекулярная масса олова 119.

Решение. Для решения необходимо использовать уравнение Клаузиуса – Клапейрона: dP dT = Δ ф.п. S ¯ Δ ф.п. V ¯ = Δ ф.п. H ¯ T ф.п. Δ ф.п. V ¯ = Δ пл H ¯ T пл M( 1 ρ ж − 1 ρ тв ) MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGKbGaamiuaaqaaiaadsgacaWGubaaaiabg2da9maalaaabaGaeuiLdq0aaSbaaSqaaiaadsebcaGGUaGaam4peiaac6caaeqaaOWaa0aaaeaacaWGtbaaaaqaaiabfs5aenaaBaaaleaacaWGerGaaiOlaiaad+dbcaGGUaaabeaakmaanaaabaGaamOvaaaaaaGaeyypa0ZaaSaaaeaacqqHuoardaWgaaWcbaGaamireiaac6cacaWG=qGaaiOlaaqabaGcdaqdaaqaaiaadIeaaaaabaGaamivamaaBaaaleaacaWGerGaaiOlaiaad+dbcaGGUaaabeaakiabfs5aenaaBaaaleaacaWGerGaaiOlaiaad+dbcaGGUaaabeaakmaanaaabaGaamOvaaaaaaGaeyypa0ZaaSaaaeaacqqHuoardaWgaaWcbaGaam4peiaadUdbaeqaaOWaa0aaaeaacaWGibaaaaqaaiaadsfadaWgaaWcbaGaam4peiaadUdbaeqaaOGaamytamaabmaabaWaaSaaaeaacaaIXaaabaGaeqyWdi3aaSbaaSqaaiaadAdbaeqaaaaakiabgkHiTmaalaaabaGaaGymaaqaaiabeg8aYnaaBaaaleaacaWGcrGaamOmeaqabaaaaaGccaGLOaGaayzkaaaaaaaa@686A@ .

dP dT = 1 0.0032 бар/К=3,12⋅ 10 7 Па/К; MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaWaaSaaaeaacaWGKbGaamiuaaqaaiaadsgacaWGubaaaiabg2da9maalaaabaGaaGymaaqaaiaaicdacaGGUaGaaGimaiaaicdacaaIZaGaaGOmaaaacaqGXqGaaeimeiaabcebcaqGVaGaaeOgeiabg2da9iaaiodacaGGSaGaaGymaiaaikdacqGHflY1caaIXaGaaGimamaaCaaaleqabaGaaG4naaaakiaab+bbcaqGWqGaae4laiaabQbbcaGG7aaaaa@4F40@        Δ пл H ¯ =7,2 кДж/моль MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaad+dbcaWG7qaabeaakmaanaaabaGaamisaaaacqGH9aqpcaaI3aGaaiilaiaaikdacaaMe8UaaeOoeiaabsbbcaqG2qGaae4laiaabYdbcaqG+qGaae4oeiaabYebaaa@449B@ ;

T_пл = 505 K; M = 0.119 кг/моль; ρ ж MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaSbaaSqaaiaadAdbaeqaaaaa@3898@ = 6,988 10³ кг/м³

Отсюда следует ответ: ρ тв MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaSbaaSqaaiaadkebcaWGYqaabeaaaaa@395F@ = 7,18 10³ кг/м³

Обратите внимание: в справочнике при 298 К ρ тв MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaSbaaSqaaiaadkebcaWGYqaabeaaaaa@395F@ = 7,37 10³ кг/м³.
Найденная нами величина – это плотность при Т_пл = 505 K. Коэффициент теплового расширения (298 К) <α_L(Sn) = 2,2^.10^–5 K^–1.
Из этой величины ρ тв MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaSbaaSqaaiaadkebcaWGYqaabeaaaaa@395F@ (505 K) = ρ тв MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqyWdi3aaSbaaSqaaiaadkebcaWGYqaabeaaaaa@395F@ (298 K)^.0,986 = 7,26^.10³ кг/м³.
Причина несовпадения на 40 % по Δ_плV – приближенность линейной аппроксимации t(P) в условии задачи

153. (4/2-03). Равновесное давление пара над сконденсированным газом В равно 38 бар при 22 °С. Зависимость коэффициента активности нелетучего растворителя А от состава бинарного жидкого раствора, образованного веществами А и В, при этой температуре описывается уравнением ln⁡ γ A =−0,1 x B 2 −0,8 x B 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaamyqaaqabaGccqGH9aqpcqGHsislcaaIWaGaaiilaiaaigdacaWG4bWaa0baaSqaaiaadkeaaeaacaaIYaaaaOGaeyOeI0IaaGimaiaacYcacaaI4aGaamiEamaaDaaaleaacaWGcbaabaGaaG4maaaaaaa@470A@ . Определите численное значение константы Генри. Определите состав раствора, находящего в равновесии с газом В, если парциальное давление последнего равно 76 торр.

Решение:

Из выражения для коэффициента активности γ₁ компонента 1 бинарного раствора, используя уравнение Гиббса – Дюгема x 1 dln⁡ γ 1 + x 2 dln⁡ γ 2 =0 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaakiaadsgaciGGSbGaaiOBaiabeo7aNnaaBaaaleaacaaIXaaabeaakiabgUcaRiaadIhadaWgaaWcbaGaaGOmaaqabaGccaWGKbGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaaIWaaaaa@4737@ , можно вывести выражение для γ₁.

Выведем это выражение в общем виде для ln⁡ γ 1 = b 1 x 2 2 + c 1 x 2 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaWGIbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaDaaaleaacaaIYaaabaGaaGOmaaaakiabgUcaRiaadogadaWgaaWcbaGaaGymaaqabaGccaWG4bWaa0baaSqaaiaaikdaaeaacaaIZaaaaaaa@4551@ .

x 1 dln⁡ γ 1 + x 2 dln⁡ γ 2 = x 1 (2 b 1 x 2 +3 c 1 x 2 )d x 2 + x 2 dln⁡ γ 2 =0 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaakiaadsgaciGGSbGaaiOBaiabeo7aNnaaBaaaleaacaaIXaaabeaakiabgUcaRiaadIhadaWgaaWcbaGaaGOmaaqabaGccaWGKbGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiikaiaaikdacaWGIbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaBaaaleaacaaIYaaabeaakiabgUcaRiaaiodacaWGJbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaDaaaleaadaWgaaadbaGaaGOmaaqabaaaleaacaaIYaaaaOGaaiykaiaadsgacaWG4bWaaSbaaSqaaiaaikdaaeqaaOGaey4kaSIaamiEamaaBaaaleaacaaIYaaabeaakiaadsgaciGGSbGaaiOBaiabeo7aNnaaBaaaleaacaaIYaaabeaakiabg2da9iaaicdaaaa@6172@

dln⁡ γ 2 =−(2 b 1 x 1 +3 c 1 x 1 x 2 )d x 2 =(2 b 1 x 1 +3 c 1 x 1 (1− x 1 ))d x 1 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamizaiGacYgacaGGUbGaeq4SdC2aaSbaaSqaaiaaikdaaeqaaOGaeyypa0JaeyOeI0IaaiikaiaaikdacaWGIbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaBaaaleaacaaIXaaabeaakiabgUcaRiaaiodacaWGJbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaBaaaleaacaaIXaaabeaakiaadIhadaWgaaWcbaGaaGOmaaqabaGccaGGPaGaamizaiaadIhadaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaGGOaGaaGOmaiaadkgadaWgaaWcbaGaaGymaaqabaGccaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaey4kaSIaaG4maiaadogadaWgaaWcbaGaaGymaaqabaGccaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiikaiaaigdacqGHsislcaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiaacMcacaWGKbGaamiEamaaBaaaleaacaaIXaaabeaaaaa@6151@

ln⁡ γ 2 = ∫ (−3 c 1 x 1 2 +(2 b 1 +3 c 1 ) x 1 )d x 1 = ( b 1 + 3 2 c 1 ) x 1 2 −3 c 1 x 1 3 +C MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpdaWdbaqaaiaacIcacqGHsislcaaIZaGaam4yamaaBaaaleaacaaIXaaabeaakiaadIhadaqhaaWcbaGaaGymaaqaaiaaikdaaaGccqGHRaWkcaGGOaGaaGOmaiaadkgadaWgaaWcbaGaaGymaaqabaGccqGHRaWkcaaIZaGaam4yamaaBaaaleaacaaIXaaabeaakiaacMcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaaiykaiaadsgacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeyypa0daleqabeqdcqGHRiI8aOGaaiikaiaadkgadaWgaaWcbaGaaGymaaqabaGccqGHRaWkdaWcaaqaaiaaiodaaeaacaaIYaaaaiaadogadaWgaaWcbaGaaGymaaqabaGccaGGPaGaamiEamaaDaaaleaacaaIXaaabaGaaGOmaaaakiabgkHiTiaaiodacaWGJbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaDaaaleaacaaIXaaabaGaaG4maaaakiabgUcaRiaadoeaaaa@6507@

При x 1 →0,  γ 2 →1,ln⁡ γ 2 →0 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaakiabgkziUkaaicdacaGGSaGaaGPaVlabeo7aNnaaBaaaleaacaaIYaaabeaakiabgkziUkaaigdacaGGSaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGHsgIRcaaIWaaaaa@49D2@ и, следовательно, С = 0.

ln⁡ γ 2 = b 2 x 1 2 + c 2 x 1 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaWGIbWaaSbaaSqaaiaaikdaaeqaaOGaamiEamaaDaaaleaacaaIXaaabaGaaGOmaaaakiabgUcaRiaadogadaWgaaWcbaGaaGOmaaqabaGccaWG4bWaa0baaSqaaiaaigdaaeaacaaIZaaaaaaa@4552@ , b 2 = b 1 + 3 2 c 1 , c 2 =− c 1 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaaIYaaabeaakiabg2da9iaadkgadaWgaaWcbaGaaGymaaqabaGccqGHRaWkdaWcaaqaaiaaiodaaeaacaaIYaaaaiaadogadaWgaaWcbaGaaGymaaqabaGccaGGSaGaam4yamaaBaaaleaacaaIYaaabeaakiabg2da9iabgkHiTiaadogadaWgaaWcbaGaaGymaaqabaaaaa@4534@ .

Для условия данной задачи ln⁡ γ B =−0,7 x A 2 +0,8 x A 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaamOqaaqabaGccqGH9aqpcqGHsislcaaIWaGaaiilaiaaiEdacaWG4bWaa0baaSqaaiaadgeaaeaacaaIYaaaaOGaey4kaSIaaGimaiaacYcacaaI4aGaamiEamaaDaaaleaacaWGbbaabaGaaG4maaaaaaa@4704@ .

Константа Генри – это значение в предельно разбавленном растворе
K Г = lim⁡ x B →0 ( P B 0 γ B )= lim⁡ x A →1 ( P B 0 γ B )=exp⁡(0,1) P B 0 =42  атм. MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4samaaBaaaleaacaWGtqaabeaakiabg2da9maaxababaGaciiBaiaacMgacaGGTbaaleaacaWG4bWaaSbaaWqaaiaadkeaaeqaaSGaeyOKH4QaaGimaaqabaGcdaqadaqaaiaadcfadaqhaaWcbaGaamOqaaqaaiaaicdaaaGccqaHZoWzdaWgaaWcbaGaamOqaaqabaaakiaawIcacaGLPaaacqGH9aqpdaWfqaqaaiGacYgacaGGPbGaaiyBaaWcbaGaamiEamaaBaaameaacaWGbbaabeaaliabgkziUkaaigdaaeqaaOWaaeWaaeaacaWGqbWaa0baaSqaaiaadkeaaeaacaaIWaaaaOGaeq4SdC2aaSbaaSqaaiaadkeaaeqaaaGccaGLOaGaayzkaaGaeyypa0JaciyzaiaacIhacaGGWbGaaiikaiaaicdacaGGSaGaaGymaiaacMcacaWGqbWaa0baaSqaaiaadkeaaeaacaaIWaaaaOGaeyypa0JaaGinaiaaikdacaaMc8UaaGPaVlaabcdbcaqGcrGaaeipeiaac6caaaa@68F2@

161. (3/2-05).* Найти работу разделения эквимолярной бинарной неидеальной смеси на чистые компоненты при 298 К и атмосферном давлении, если известно, что логарифм коэффициента активности γ₁ для этой смеси зависит от состава согласно уравнению:

ln⁡ γ 1 = b 1 x 2 2 + c 1 x 2 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaWGIbWaaSbaaSqaaiaaigdaaeqaaOGaamiEamaaDaaaleaacaaIYaaabaGaaGOmaaaakiabgUcaRiaadogadaWgaaWcbaGaaGymaaqabaGccaWG4bWaa0baaSqaaiaaikdaaeaacaaIZaaaaaaa@4551@ , где b 1 =0,5, c 1 =1. MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaaIXaaabeaakiabg2da9iaaicdacaGGSaGaaGynaiaacYcacaWGJbWaaSbaaSqaaiaaigdaaeqaaOGaeyypa0JaaGymaiaac6caaaa@3FF0@

Решение. Из выражения для коэффициента активности γ₁ компонента 1 бинарного раствора, используя уравнение Гиббса – Дюгема x 1 dln⁡ γ 1 + x 2 dln⁡ γ 2 =0 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEamaaBaaaleaacaaIXaaabeaakiaadsgaciGGSbGaaiOBaiabeo7aNnaaBaaaleaacaaIXaaabeaakiabgUcaRiaadIhadaWgaaWcbaGaaGOmaaqabaGccaWGKbGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaaIWaaaaa@4737@ ,

можно вывести выражение для γ₂ (см. выше решение задачи 155).

ln⁡ γ 2 = b 2 x 1 2 + c 2 x 1 3 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gacqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaWGIbWaaSbaaSqaaiaaikdaaeqaaOGaamiEamaaDaaaleaacaaIXaaabaGaaGOmaaaakiabgUcaRiaadogadaWgaaWcbaGaaGOmaaqabaGccaWG4bWaa0baaSqaaiaaigdaaeaacaaIZaaaaaaa@4552@ , b 2 = b 1 + 3 2 c 1 , c 2 =− c 1 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaaIYaaabeaakiabg2da9iaadkgadaWgaaWcbaGaaGymaaqabaGccqGHRaWkdaWcaaqaaiaaiodaaeaacaaIYaaaaiaadogadaWgaaWcbaGaaGymaaqabaGccaGGSaGaam4yamaaBaaaleaacaaIYaaabeaakiabg2da9iabgkHiTiaadogadaWgaaWcbaGaaGymaaqabaaaaa@4534@ .

Для условия этой задачи b 2 =2, c 2 =−1 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOyamaaBaaaleaacaaIYaaabeaakiabg2da9iaaikdacaGGSaGaam4yamaaBaaaleaacaaIYaaabeaakiabg2da9iabgkHiTiaaigdaaaa@3EC0@ . Для эквимолярной смеси

ln⁡ γ 1 =0,5 x 2 2 + x 2 3 =0,25,  ln⁡ γ 2 =2 x 1 2 − x 1 3 =0,375 γ 1 =1,28,  γ 2 =1,455. MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaaciGGSbGaaiOBaiabeo7aNnaaBaaaleaacaaIXaaabeaakiabg2da9iaaicdacaGGSaGaaGynaiaadIhadaqhaaWcbaGaaGOmaaqaaiaaikdaaaGccqGHRaWkcaWG4bWaa0baaSqaaiaaikdaaeaacaaIZaaaaOGaeyypa0JaaGimaiaacYcacaaIYaGaaGynaiaacYcacaaMf8UaaGzbVlGacYgacaGGUbGaeq4SdC2aaSbaaSqaaiaaikdaaeqaaOGaeyypa0JaaGOmaiaadIhadaqhaaWcbaGaaGymaaqaaiaaikdaaaGccqGHsislcaWG4bWaa0baaSqaaiaaigdaaeaacaaIZaaaaOGaeyypa0JaaGimaiaacYcacaaIZaGaaG4naiaaiwdaaeaacqaHZoWzdaWgaaWcbaGaaGymaaqabaGccqGH9aqpcaaIXaGaaiilaiaaikdacaaI4aGaaiilaiaaywW7cqaHZoWzdaWgaaWcbaGaaGOmaaqabaGccqGH9aqpcaaIXaGaaiilaiaaisdacaaI1aGaaGynaiaac6caaaaa@6D7E@

A=− G M =−RT( x 1 ln⁡ x 1 γ 1 + x 2 ln⁡ x 2 γ 2 )=0,068RT=168,4 MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyqaiabg2da9iabgkHiTiaadEeadaahaaWcbeqaaiaad2eaaaGccqGH9aqpcqGHsislcaWGsbGaamivaiaacIcacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaciiBaiaac6gacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeq4SdC2aaSbaaSqaaiaaigdaaeqaaOGaey4kaSIaamiEamaaBaaaleaacaaIYaaabeaakiGacYgacaGGUbGaamiEamaaBaaaleaacaaIYaaabeaakiabeo7aNnaaBaaaleaacaaIYaaabeaakiaacMcacqGH9aqpcaaIWaGaaiilaiaaicdacaaI2aGaaGioaiaadkfacaWGubGaeyypa0JaaGymaiaaiAdacaaI4aGaaiilaiaaisdaaaa@5C19@ Дж/моль

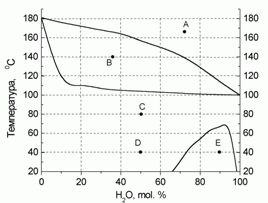180. (4/2-05).* На рисунке приведена диаграмма состояния “температура – состав” для системы вода-фенол при давлении 760 торр. Определите, какие и какого состава фазы присутствуют в системе в точках А – Е. Нарисуйте схематично диаграмму при P = 100 торр.
Для воды D _испН = 40,66 кДж/моль (t_кип = 100 ^оС).
Для фенола D _испН = 47,97 кДж/моль (t_кип = 181,9 ^оС).

Решение:

А – пар ~ 70 % Н₂О.

В – пар ~ 70 % Н₂О и раствор воды в феноле (x(Н₂О) ~ 5 %).

С – раствор (x(Н₂О) ~ 50 %)

D = С

E – раствор фенола в воде (x(H₂O) ~ 96 %) и раствор воды в феноле (x(Н₂О) ~ 73 %).

При давлении 100 торр температуры кипения чистых компонентов можно оценить по формуле

ln⁡( P 2 P 1 )=− Δ исп H R ( 1 T 2 − 1 T 1 ), MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaciiBaiaac6gadaqadaqaamaalaaabaGaamiuamaaBaaaleaacaaIYaaabeaaaOqaaiaadcfadaWgaaWcbaGaaGymaaqabaaaaaGccaGLOaGaayzkaaGaeyypa0JaeyOeI0YaaSaaaeaacqqHuoardaWgaaWcbaGaamioeiaadgebcaWG=qaabeaakiaadIeaaeaacaWGsbaaamaabmaabaWaaSaaaeaacaaIXaaabaGaamivamaaBaaaleaacaaIYaaabeaaaaGccqGHsisldaWcaaqaaiaaigdaaeaacaWGubWaaSbaaSqaaiaaigdaaeqaaaaaaOGaayjkaiaawMcaaiaacYcaaaa@4CDE@ которая получается интегрированием уравнения Клапейрона – Клаузиуса для фазового перехода “жидкость–пар” в приближении Δ исп H MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeuiLdq0aaSbaaSqaaiaadIdbcaWGbrGaam4peaqabaGccaWGibaaaa@3AA9@ = const.

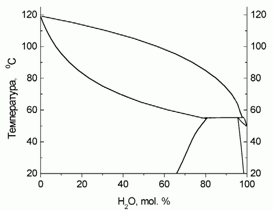
Подставляя данные из задачи, получаем

T_кип(H₂O, 100 торр) = 323 K, T_кип(фенол, 100 торр) = 392,2 K

Зависимостью растворимости жидкостей друг в друге от давления можно пренебречь.

Диаграмма при P = 100 торр приведена на рисунке:

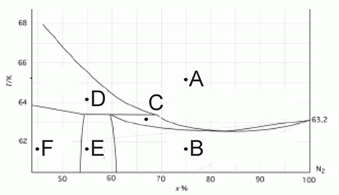
203. (5/2-07). На рисунке представлена фазовая диаграмма T(x) для бинарной системы “Ar – N₂” в области фазовых переходов твердое – жидкость
(T указана в К).
Опишите фазовый состав в точках А–F.

Решение. A – жидкий раствор аргона в азоте (х(N₂) = 75 %)

В – твердый раствор Т1 аргона в азоте (х(N₂) = 75 %)

С – 2 фазы: жидкость с х(N₂) ~ 70 % и твердое Т1 с х(N₂) ~ 62 %

соотношение Ж/Т1 ~ (67–62)/(70–67) = 5/3

D – 2 фазы: жидкость с х(N₂) ~ 63 % и твердое Т2 с х(N₂) ~ 40 %

соотношение Ж/Т2 ~ (55–40)/(63–55) = 15/8

E – 2 фазы: твердое Т1 с х(N₂) ~ 61 % и твердое Т2 с х(N₂) ~ 54 %

соотношение Т1/Т2 ~ (55–54)/(61–55) = 1/6

F – 1 фаза: твердый раствор Т2 азота в аргоне (х(N₂) = 45 %)

При анализе диаграммы необходимо учесть, что в соответствии с правилом фаз Гиббса линия солидуса – горизонтальная прямая, если в граничащих областях диаграммы существуют 3 фазы (например, в области D – Ж и Т2, а в области С – Ж и Т1). Если же линия солидуса – кривая, то в граничащих областях существуют только 2 фазы (например, по этой причине область B может быть только однофазной и содержит твердый раствор Т1).

214. (2/2-07).* Для выделения чистой воды из морской вблизи берега моря вырыт колодец, стенки которого выполнены из материала, который можно рассматривать как идеальную селективную по воде мембрану, проницаемую для воды и не пропускающую растворенные в морской воде соли. Рассчитайте КПД такого способа. Мольную долю ионов в морской воде можно полагать равной 2 %.

Решение. Уровень воды в колодце ниже, чем в море из-за осмотического давления π. Работа, которую необходимо совершить для выделения 1 моля чистой воды, – это работа на подьём воды из колодца на высоту h= π ρg MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiAaiabg2da9maaliaabaGaeqiWdahabaGaeqyWdiNaam4zaaaaaaa@3C5B@ против силы тяжести F=gρ V ¯ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOraiabg2da9iaadEgacqaHbpGCdaqdaaqaaiaadAfaaaaaaa@3B56@ . Если КПД насоса η, то совершенная работа составит
W=ηπ V ¯ =η( CRT ) V ¯ =η( x V ¯ RT ) V ¯ =ηxRT MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaam4vaiabg2da9iabeE7aOjabec8aWnaanaaabaGaamOvaaaacqGH9aqpcqaH3oaAdaqadaqaaiaadoeacaWGsbGaamivaaGaayjkaiaawMcaamaanaaabaGaamOvaaaacqGH9aqpcqaH3oaAdaqadaqaamaalaaabaGaamiEaaqaamaanaaabaGaamOvaaaaaaGaamOuaiaadsfaaiaawIcacaGLPaaadaqdaaqaaiaadAfaaaGaeyypa0Jaeq4TdGMaamiEaiaadkfacaWGubaaaa@51F2@

(необходимо, конечно, помнить, что это уравнение для осмоса работает при мольной доле π= RTln⁡(1−x) V ¯ MathType@MTEF@5@5@+=feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=xfr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaeqiWdaNaeyypa0ZaaSaaaeaacaWGsbGaamivaiGacYgacaGGUbGaaiikaiaaigdacqGHsislcaWG4bGaaiykaaqaamaanaaabaGaamOvaaaaaaaaaa@413E@ ).

Минимальная требуемая работа для выделения пресной воды из морской:

Следовательно, КПД предлагаемого способа – это КПД насоса, который качает воду из колодца.