1. ФОРМАЛЬНАЯ КИНЕТИКА

1.3. Интегрирование кинетических уравнений

Кинетические схемы с несколькими стадиями.
Параллельные и последовательные реакции

1.3.28. Получите выражения зависимостей концентраций A, B и C от времени и определите время достижения максимальной концентрации промежуточного вещества В для реакции, описывающейся кинетической схемой

А В С,

если k₁= 10^–2 c^–1, k₂ = 3 × 10^–2 c^–1. При t = 0 [A] = [A]₀, [B] = [C] = 0.

Какое относительное количество вещества В следует добавить в исходное вещество А, чтобы время достижения максимальной концентрации вещества [B]_max уменьшилось вдвое?

1.3.29. (КР1–2005, № 1). Метилфенилсульфид может реагировать с Н₂О₂ по схеме

PhSMe + H₂O₂ PhSOMe + H₂O.

Образующийся сульфоксид может в дальнейшем окисляться до сульфона:

PhSOMe + H₂O₂ PhSO₂Me + H₂O.

k₁ = 1,5 × 10^–3 М^–1с^–1, k₂ = 0,2 × 10^–3 М^–1с^–1, начальная концентрация сульфида равна C₀, перекись взята в большом избытке.

Определите концентрации сульфида, сульфоксида и сульфона в момент, когда концентрация сульфоксида достигнет максимума.

1.3.30. (КР1–2001, № 4). Изотопный обмен дейтерия, растворённого в воде, протекает при определённых условиях по механизму:

D₂ +H₂O HD + HDO

HD + H₂O H₂ +HDO.

Найдите зависимость концентрации HD от времени. [D₂]₀ = 10^–3 M, [HD]₀ = 10^–4 M, k₁ = 2 k₂.

1.3.31. (КР1–2003, № 1). Дейтерированный алкиламин взаимодействует с большим избытком воды по схеме:

RND₂ + H₂O RNHD + HDO,

RNHD + H₂O RNH₂ + HDO.

Найдите максимальную концентрацию RNHD, если k₁ = 2 k₂, а в начальный момент времени в системе был только дейтерированный алкиламин с концентрацией X₀.

1.3.32. Для реакции, протекающей по механизму

X Y Z,

найдите зависимость от времени концентраций веществ X, Y и Z, если известны начальные концентрации веществ C_X⁽⁰⁾ = a, C_Y⁽⁰⁾ = 0, C_Z⁽⁰⁾ = 0.

1.3.33. (КР1–2008, № 5). Найдите кинетические кривые для всех веществ, участвующих в последовательных мономолекулярных превращениях

A B C D E G,

если в начальный момент времени в системе присутствует только вещество А с концентрацией a.

1.3.34. Получите выражения зависимостей концентраций A, B, C и D от времени для реакции, описывающейся кинетической схемой

при начальных условиях t = 0, [A] = A₀, [B] = [C] = [D] = 0.

1.3.35. Получите выражения зависимостей концентраций A, B, C и D от времени для реакции, описывающейся кинетической схемой

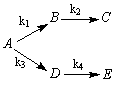
при начальных условиях t = 0, [A] = A₀, [B] = [C] = [D] = [E] = 0.

1.3.36. Выведите кинетические уравнения для расходования вещества A и накопления веществ B и C, участвующих в реакции

B A C.

Начальные концентрации веществ: C_A(0) = С₀, C_B(0) = C_С(0) = 0.

1.3.37. Для реакции, протекающей по механизму

A B P,

найдите концентрации С_А, C_B и C_Р веществ A, B и Р, как функции времени, если начальные концентрации C_A(0) = C_B(0) = C_P(0) = C₀.

Изобразите качественно графики функций C_A(t), C_B(t) и C_P(t) для случая k_–1 >> k₁ >> k₂.

1.3.38. Найдите точное решение прямой кинетической задачи для реакции, протекающей по механизму

А В С,

в случае, когда = а, = = 0.

1.3.39. Кинетика гидрирования нитрохлорбензола в избытке водорода соответствует следующей схеме:

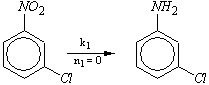
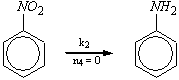
Здесь k_i (i = 1¸4) – эффективные константы скорости стадий реакции, n_i (i = 1¸4) – наблюдаемые порядки реакции по превращаемому реагенту. Найдите время полного превращения исходного нитрохлорбензола и концентрации всех продуктов в этот момент времени.

1.3.40. (Пе1–2007, № 2). Превращение реагента А протекает по трем параллельным реакциям

1) A B,

2) A C,

3) A D.

Эффективная константа скорости реакции k = k₁ + k₂ + k₃ при температурах 460 и 520 °С составила соответственно 17 и 56,5 с^–1. При этом соотношение концентраций продуктов [В] : [С] : [D] не зависело от температуры. Найдите энергии активации всех стадий.

1.3.41. В системе протекают две параллельные реакции по уравнениям:

A + 2 C D,

В + 2 C E.

Отношение k₁/k₂ = 5. Сколько процентов вещества В прореагирует к моменту времени, когда вещество А будет израсходовано на 95 %, если вещество С находится в избытке? Начальные концентрации А и В равны.

1.3.42. Для схемы, приведенной в предыдущей задаче, рассчитайте процент превращения вещества B к моменту времени, когда вещество А будет израсходовано на 90 %, если k₁/k₂ = 10. Вещество С находится в избытке.

1.3.43. Вещество А по двум параллельным процессам первого порядка необратимо превращается в В и С:

1) А ¾® В,

2) А ¾® С.

Константа скорости реакции (2) в 100 раз меньше, чем константа скорости реакции (1). Через 25 мин концентрация В составила 75 % от . Через какое время C_B будет равна 75 % от ? (и – концентрации С и В при t ® ¥)?

1.3.44. (КР1–2007, № 4). Реакция разложения изопропилового спирта протекает по схеме

,

.

Реакция проводится в закрытом сосуде постоянного объёма. Отношение констант скорости k₁/k₂ равно 0,8. Через 60 с после начала реакции концентрация ацетона составляет 50 % от её конечного значения (т. е. значения после завершения реакции). Через какое время после начала реакции концентрация пропилена будет составлять 75 % от её конечного значения?

1.3.45. В 3,2 %-м (по весу) растворе метанола в воде образовались радикалы и в концентрации 10^–5 моль/л каждый. Радикалы гибнут по реакциям

,

,

причём k₁ = 10⁹ М^–1с^–1, k₂ = 10⁴ М^–1с^–1.

В какой из реакций погибнет большая часть радикалов ? Оцените, во сколько раз изменится концентрация радикалов к моменту полной гибели радикалов . Плотность раствора принять равной 1 г/cм³.

1.3.46. (КР1–2006, № 1). Окисление стирола нестабильным оксокомплексом хрома (V) LCr^VO протекает одновременно с дезактивацией LCr^VO. А и В – продукты превращения комплекса в реакциях окисления субстрата и авто-распада:

C₆H₅CHCH₂ + LCr^VO C₆H₅CH(O)CH₂ + А,

LCr^VO B.

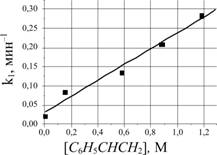
Эффективная константа k₁ скорости расходования комплекса зависит от концентрации стирола так, как показано на рисунке. Оцените константы k_A и k_B.

1.3.28. Газ А необратимо превращается одновременно по двум реакциям:

1) А ¾® В (реакция первого порядка),

2) 2 А ¾® С (реакция второго порядка).

В начальный момент в закрытом сосуде находился только газ А, причём его концентрация была такова, что скорости превращения по обоим путям были одинаковы. Найдите состав системы после окончания реакций.

1.3.29. В смеси веществ А, В, С при [А] >>([В] + [C]) протекают параллельные реакции:

1) А + В ¾® D,

2) А + С ¾® Е.

Величина k₁ равна 0,5 М^–1с^–1. К моменту полупревращения вещества В концентрация вещества С уменьшилась в 5 раз. Определите величину k₂.

1.3.30. В смеси веществ А и В протекают параллельные реакции:

1) А + В ¾® C,

2) A ¾® D.

По завершении реакции [C]_¥ = 0,9 [B]₀, [D]_¥ = 0,023 M. Определите величину отношения констант скорости реакций 1 и 2.

1.3.31. В системе протекают конкурентные реакции

1) А + В ¾® D,

2) A + C ¾® Е,

Начальные концентрации реагентов: [A]₀ = 10^–3 М; [B]₀ = 1,0 М; [C]₀ = 2 M. Конечные концентрации продуктов: [E]_µ = 1,67 × 10^–4  М; [D]_µ = 8,33 × 10^–4 M. Константа скорости k₁ = 10⁴ M^–1 c^–1. Чему равна величина k₂?

1.3.32. В реакционной газофазной системе с постоянной скоростью 10¹⁰ см^–3с^–1 образуются активные частицы Х, которые могут вступать в следующие превращения:

X A, k₁ = 7 × 10^–3 c^–1,

X + B C, k₂ = 2 × 10^–16 cм³ c^–1.

Начальная скорость образования продукта С равна 2 × 10⁹ см^–3с^–1, температура равна 320 °С. Определите начальное давление в системе, считая, что вещество В находится в большом избытке.

1.3.33. Масс-спектроскопически при 130 °С изучали скорости образования метана и этана при фотолизе газовых смесей азометана

(АМ) и метиламина (RH). В зависимости от состава смеси получено следующее:

[AM] × 10^3, моль/л	0,5	1,0	2,0	5,0	10,0
[RH] × 10^3, моль/л	0,05	0,3	1,0	4,0	10,0
WCH4× 10^9, моль/(л×с)	1,0	1,5	5,0	8,0	12,0
WC2H6× 10^9, моль/(л×с)	3,7	1,7	4,0	1,35	0,67

В этой системе метильные радикалы, образующиеся при фотолизе азометана, взаимодействуют с азометаном и метиламином с образованием метана (константы скорости k₁ и k₂), а также рекомбинируют с константой скорости k_p = 1,0 × 10⁹ М^–1c^–1. По этим экспериментальным результатам определите k₁ и k₂ (метод конкурирующих реакций).

1.3.34. С помощью импульсного фотолиза растворов дитретбутилперекиси измеряли начальные скорости гибели радикалов в зависимости от их начальной концентрации. Получены следующие результаты:

[R^·]0 × 10^5, моль/л	5	3	1	0,5	0,1
W0 × 10^3, моль/(л×с)	600	240	40	15	2,2

Гибель радикалов в данной системе обусловлена рекомбинацией (константа скорости k₂) и мономолекулярным превращением (константа скорости k₁)

.

Определите по этим результатам константы скорости k₁ и k₂.

1.3.35. (КР1–1998, № 5). Для последовательно-параллельной реакции

,

,

известны значения констант k₁ = k₂ = 10^–2 M^–1c^–1. Реакцию проводят с начальными концентрациями A₀ = 1 M, B₀ = 2 M, C₀ = D₀ = 0. Определите концентрации всех участников в момент времени, когда концентрация интермедиата C достигает максимума.

1.3.36. (КР1–2001, № 5). Для параллельно-последовательного процесса

A B C

A D

константы скорости k₁ = 10¹⁰ c^–1, k₂ = 10³ c^–1, k₃ = 4 × 10² c^–1 и константа равновесия стадии A B равна 1; [А]₀ = 10^–3 М.

Определите, в каком соотношении находятся концентрации продуктов D и C после завершения реакции. Найдите уравнение кинетической кривой для А.

1.3.37. (КР1–2002, № 2). Для следующей реакции найдите отношение концентраций продуктов D и E после окончания реакции:

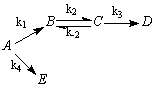
В начальный момент времени концентрация А равна А₀, а концентрации всех остальных реагентов равны нулю.

1.3.38. При облучении замороженного раствора щёлочи образуются электронные центры e_st, которые могут либо гибнуть по мономолекулярному закону , либо реагировать с молекулами закиси азота, предварительно растворённой в щёлочи:

.

Под действием одного импульса электронного ускорителя образуется 2 × 10¹⁶ электронных центров/см³. За 10⁴ импульсов (каждый последующий импульс подавали после полного исчезновения электронных центров) в образце объёмом 1 см³ образовалось
4,7 × 10^–5 моль азота. Определите отношение констант k₁/k₂, если начальная концентрация закиси азота равна 10^–2 М.

1.3.39. В водном растворе H₂SO₄ при комнатной температуре протекает окисление щавелевой кислоты комплексом Ru³⁺(bpy)₃ по брутто-реакции

.

Концентрации [Ru³⁺(bpy)₃]₀ = 5 × 10^–5 M, [H₂C₂O₄]₀ = 4 × 10^–2 M.

Известно, что лимитирующей стадией этой сложной реакции является одноэлектронное окисление комплексом молекул H₂C₂O₄ или , причём константы скорости взаимодействия Ru³⁺(bpy)₃ с этими формами щавелевой кислоты k₁ и k₂ (обе в M^–1×c^–1) различные. По какому временному закону будет происходить исчезновение Ru³⁺(bpy)₃ в этих условиях? Получите выражение для k_эф. Каким образом можно определить в эксперименте k₁ и k₂, если определена зависимость k_эф от [H⁺] при изменении [H₂SO₄] от 0,1 до 0,5 M, а также известны константы равновесия последовательной диссоциации H₂C₂O₄ K_I = 6,5 × 10^–2 M, K_II = 5,2 × 10^–5 M?

1.3.40. (КР1–2004, № 2). Вещество A может принимать участие в двух параллельных процессах:

.

Начальные концентрации равны [A]₀ = [B]₀ = a, [C]₀ = [D]₀ = 0. Найдите состав смеси после завершения реакций, если k₁ = k₂.

1.3.41. В замкнутом реакторе проводят крекинг пропана, при котором промежуточным соединением является этилен. Изменение концентрации этилена в общем случае описывается выражением dC_эт/dt = w_o – w_p, где w_o и w_p - скорости образования и расходования этилена соответственно. Для определения w_o применили метод Неймана, заключающийся в добавлении к системе малого количества радиоактивного этилена и регистрации изменения концентрации этилена С_эт в системе и молярной радиоактивности этилена b (доли радиоактивных молекул этилена). Было обнаружено, что = -2 × 10^–7 мин^–1 при С_эт = 6 × 10^–4 М. Найдите величину w_o.

1.3.42. (Экз–2008, № 1). Гидролиз дифторида ксенона в водном растворе происходит в результате последовательных реакций:

1) XeF₂ + H₂O ¾® 2 HF + XeO, k₁ × [H₂O] = 4 × 10^–4 c^–1;

2) XeO + H₂O ¾® Xe + H₂O₂, k₂ × [H₂O] = 10⁵×c^–1;

3) H₂O₂+ XeF₂ ¾® 2 HF + Xe + O₂, k₃ = 2 M^–1×c^–1.

Какая максимально возможная концентрация перекиси может достигаться в ходе этой реакции? В начальный момент времени перекись в системе отсутствовала.