1. ФОРМАЛЬНАЯ КИНЕТИКА

1.5. Приближённые методы решения кинетических уравнений. Метод квазистационарных концентраций. Квазиравновесное приближение

1.5.1. Найдите точное решение прямой кинетической задачи для реакции, протекающей по механизму

А В Х.

Покажите, как это решение переходит в приближённое решение, соответствующее методу стационарных концентраций. Начальные концентрации веществ: .

1.5.2. При каких ограничениях на концентрации и константы скорости метод стационарных концентраций применим для описания реакции

A + B 2 C D?

1.5.3. При каких соотношениях между константами можно использовать метод стационарных концентраций для описания процесса

2 A B 2 C?

1.5.4. На примере сложной реакции

А 2 В С

продемонстрируйте использование метода стационарных концентраций. Укажите условия его применимости.

1.5.5. Определите условие применимости метода стационарных концентраций для описания кинетики сложной реакции

3 А 2 В 2 С.

Начальные концентрации веществ C_A⁰ = a, C_B⁰ = C_C⁰ = 0.

1.5.6. Определите условие применимости метода стационарных концентраций для описания кинетики сложной реакции

А + 2 В 2 С,

C + D P,

если причём a >> b.

1.5.7. При каких соотношениях между константами можно использовать метод стационарных концентраций для описания процесса

A 2 B C?

1.5.8. Выведите условие применимости метода стационарных концентраций для описания кинетики реакции, протекающей по механизму

2 A B X.

Какой порядок имеет эта реакция в стационарных условиях? Как её эффективная константа скорости связана с константами скорости отдельных стадий? Какому режиму протекания реакции соответствует случай k₂ << k_–1?

1.5.9. Определите условие применимости метода стационарных концентраций для описания кинетики сложной реакции

A + B C,

C + D P,

если причём a >> b.

1.5.1. Превращение изотопа ²³⁸U в изотоп ²³⁴U состоит из трёх последовательных ядерных реакций:

Какова будет доля ²³⁴Th в смеси изотопов ²³⁸U, ²³⁴Th, ²³⁴Pa и ²³⁴U через 10, 20, 40 и 80 дней после начала распада чистого ²³⁸U? Через t_1/2 обозначены времена полураспада изотопов.

1.5.2. Реакция выделения H₂ из растворов дважды восстановленных форм KH₂ гетерополикислот идёт по механизму

KH₂ K + H₂,

K + KH₂ 2 KH,

где K – активное промежуточное вещество.

Найдите выражения для изменения концентраций веществ KH₂ и H₂ во времени. Чему равна константа скорости k₁, если время полупревращения вещества KH₂ равно 20 мин?

Найдите условие применимости метода стационарных концентраций для рассматриваемой реакции. Каково время установления стационарной концентрации вещества K?

1.5.3. Реакция перекиси водорода с ионами Fe²⁺ происходит по схеме

Константы скоростей стадий приведены в таблице:

k1	k2	k3	k4
10 M^–1с^–1	10^9 M^–1с^–1	10^–10 см^3/с	10^–12 cм^3/с

Найдите выражения для скоростей выделения О₂ и расходования Fe²⁺ и Н₂О₂, полагая, что радикалы и очень реакционноспособны. В каком диапазоне могут изменяться порядки реакций по Fe²⁺ и Н₂О₂? Найдите стационарные концентрации частиц и и численные значения скоростей стадий, если начальные концентрации реагентов равны [H₂O₂]₀ = 0,1 М, [Fe²⁺]₀ = 10¹⁵ см^–3.

1.5.4. Термическое разложение гидроперекиси ROOH протекает по механизму

, k₁ = 10^–4 c^–1,

, k₂ = 10⁵ M^–1c^–1,

, k₃ = 10⁴ M^–1c^–1,

, k₄ = 10⁷ M^–1c^–1.

Определите квазистационарные концентрации промежуточных частиц и скорость разложения гидроперекиси при C_ROOH = 0,1 M. Выведите условия применимости метода квазистационарных концентраций в данном случае.

1.5.5. Окисление гидрохинона (QH₂) хлорноватистой кислотой в буферном растворе (рН > 7) протекает по следующему механизму:

1) ,

2) .

Найдите зависимость концентрации от времени, если известно, что характерное время установления равновесия (2) много меньше характерного времени реакции (1), и равновесие (2) сильно сдвинуто влево в сторону QH₂ и Q. Гидрохинон взят в большом избытке [QH₂]₀ >> [HOCl]₀.

1.5.6. Механизм окислительно-восстановительного взаимодействия V³⁺ и Cr²⁺ в водных растворах в общих чертах описывается следующей схемой:

V³⁺ + Cr²⁺ + H₂O [V(OH)Cr]⁴⁺ + H⁺,

[V(OH)Cr]⁴⁺ V²⁺ + Cr(OH)²⁺,

Cr(OH)²⁺ + H⁺ Cr³⁺ + H₂O (быстрое равновесие).

Получите зависимость скорости восстановления ванадия и скорости накопления Cr³⁺ от [H⁺], считая, что [V(OH)Cr]⁴⁺ – высокореакционноспособная частица.

1.5.16. При холоднопламенном окислении бутана углекислый газ может получаться как при окислении СО (со скоростью W₁), так и за счёт распада ацильных перекисных радикалов на СО₂ и радикалы RO^· (скорость W₂). Определите отношение скоростей этих процессов из результатов следующего эксперимента (кинетический изотопный метод). Сразу после установления стационарного режима реакции в реагирующую смесь добавили некоторое количество СО, меченого радиоактивными атомами ¹⁴С, так, что ее полная радиоактивность составила 75 мКюри/моль. В дальнейшем отдельно измеряли радиоактивность СО₂, образующегося в ходе окисления. Её значение на начальном этапе реакции составило 3 мКюри/моль.

Какое заключение о механизме реакции можно было бы сделать, если бы в этом эксперименте радиоактивности СО и СО₂ в тех же условиях оказались равными?

1.5.17. Окисление органического соединения A комплексами Pd(II) в водных растворах описывается схемой

1) ,

2) .

Получите выражение для кинетической кривой накопления , если известно, что степень превращения A и Pd(II) очень мала, а характерное время установления равновесия (2) много меньше характерного времени установления равновесия (1).

1.5.18. Реакция А + B ¾® D осуществляется в результате двух последовательных стадий:

1) А Х,

2) Х + B D.

Получите выражение, описывающее зависимость концентрации вещества D от времени, если реакция (2) медленная, а стадия (1) практически равновесная; [A]₀ = a, [B]₀ = a, [D]₀ = 0.

1.5.19. Разложение N₂O₅ в газовой фазе описывается схемой

1) N₂O₅ NO₂ + NO₃,

2) NO₃ ¾® NO + O₂.

Получите выражение для скорости реакции как функции концентрации N₂O₅ и NO₂ в квазистационарном и квазиравновесном приближении. Определите условия применимости этих приближений в каждом случае.

1.5.20. Разложение NO₂Cl протекает по механизму

1) NO₂Cl ¾® NO₂ + Cl,

2) Cl + NO₂Cl ¾® NO₂ + Cl₂.

Получите выражение для скорости реакции в квазистационарном приближении.

1.5.21. Синтез фосгена по реакции CO + Cl₂ ¾® COCl₂ протекает по механизму

Cl₂ 2

+ CO

+ Cl₂ COCl₂ +

Выведите выражение для скорости реакции, если известно, что и являются высокореакционноспособными частицами. Каковы условия применимости предлагаемых вами приближений?

1.5.22. Реакция распада озона 2 O₃ ¾® 3 O₂ происходит по механизму

O₃ + M O₂ + O + M,

O + O₃ 2 O₂.

Пользуясь методом стационарных концентраций, выведите уравнение для скорости реакции. Чему равен порядок реакции по озону и веществу М в предельных случаях k₂[O₃] >> k_–1[O₂][M] и k₂[O₃] << k_–1[O₂][M]?

1.5.23. В результате исследования кинетических закономерностей реакции окислительного хлорирования ацетилена в водных растворах CuCl₂ и CuCl установлено, что суммарный порядок реакции при некоторых условиях равен 3.

Объясните этот факт исходя из следующей кинетической схемы

1) A + CuCl X₁ + HCl,

2) X₁ + 2 CuCl₂ ¾® X₂ + CuCl,

3) X₂ ¾® P + 2 CuCl.

Здесь А – ацетилен, Р – продукт RCºCCl, а Х₁, Х₂ – промежуточные вещества.

1.5.24. (КР1–1997, № 5). Взаимодействие атомарного кислорода с формальдегидом включает реакции:

1) , 2) ,

3) , 4) .

При начальных условиях [CH₂O] = 10¹⁶ см^–3, [O] = 2 × 10¹³ см^–3 было получено, что [CO₂] = 4 × 10¹¹ см^–3, если отношение [O]/[O]₀ = 0,68.

Принимая, что и квазистационарны, вычислите значение k₂/k₃ и найдите уравнение кинетической кривой для О.

1.5.25. (КР1–1998, № 1). Для реакции, идущей по механизму

A B C D,

найдите концентрацию вещества С в зависимости от времени в квазиравновесном приближении, если C_A⁰ = a, C_B⁰ = C_C⁰ = C_D⁰ = 0.

1.5.26. (КР1–2000, № 1). Для следующей кинетической схемы найдите зависимости от времени концентрации веществ C и B в квазиравновесном приближении:

A B C D.

Начальные концентрации равны: C_A⁰ = a, C_B⁰ = C_C⁰ = C_D⁰ = 0.

1.5.27. (КР1–2002, № 3). Найдите уравнение кинетической кривой для промежуточного продукта B, появляющегося в реакции:

(быстро, K – константа равновесия),

.

Равновесие устанавливается быстро. При t = 0 A = A₀, B = P = 0.

1.5.28. (КР1–2000, № 2). Взаимодействие СО с озоном в атмосфере кислорода при T = 100 °C протекает по механизму

O₃ + M O + O₂ + M,

O₃ + O 2 O₂,

O + CO CO₂.

Найдите зависимость скорости реакции от концентрации реагентов в квазистационарном приближении.

1.5.29. (КР1–2000, № 5). Реакция ClO₂ + Co(II) ® ClO₂^– + Co(III) в водных растворах протекает согласно следующему механизму:
1) ClO₂ + Co(II) , k₁ = 1,6 M^–1 c^–1,

2) CO(III) + Co(II) Co_a, k₂ = 0,5 M^–1 c^–1, k_–2 = 0,1 c^–1,

3) ClO₂(III) + Co_a , k₃ = 1,1 × 10³ M^–1 c^–1,

где Co_a – комплекс неопределённой структуры, [Co(II)]⁰ = 2 × 10^–4 M, [ClO₂]₀ = 2 × 10^–4 M. Определите скорость реакции в момент времени, когда [Co(II)] = 10^–4 M. Справедливо ли применение метода стационарных концентраций в данном случае?

1.5.30. (Экз–2003, № 4). Вещество X в водном растворе представлено в двух таутомерных формах А и В, которые находятся в равновесии (К = 0,25). Обе формы претерпевают мономолекулярные превращения по схеме

(k₁ = 0,1 мин^–1, k₂ = 0,6 мин^–1).

В начальный момент времени был приготовлен водный раствор X с концентрацией 0,74 М, найдите концентрацию X через 10 мин.

1.5.31. (КР1–2004, № 1). Гидролиз изоцианатов может протекать по одному из двух механизмов, в каждом из которых лимитирующей стадией является образование карбаминовой кислоты. Концентрации промежуточных комплексов X₁ и X₂ предполагаются квазистационарными. Р – продукты, Ac – кислота. Получите выражения для скорости реакции для двух предполагаемых механизмов.

Механизм 1 (быстро).

Механизм 2 (быстро).

1.5.32. (КР1–2003, № 2). Комплекс Co^II устойчив в растворе чистого CHCl₃. Однако если в системе присутствует метанол, то Co^II окисляется по схеме

Co^II + MeOH X^II, k₁ = 10³ M^–1c^–1, k_–1 = 10 c^–1,

X^II + O₂ X^III, k₂ = 10^–2 M^–1c^–1,

X^III P⁺ + O₂^–, k₃ = 1 c^–1,

где X^II º [Co^II(MeOH)], X^III º [Co^IIIO₂(MeOH)], P⁺ º [Co^III(MeOH)]⁺.

Не знавший об этом студент приготовил 10^–3 М раствор Co^II в хлороформе, содержащем 0,11 М метанола, и ушел на обед. Оцените, через какое время содержание кобальта (II) составит 50 % от исходного количества кобальта, если раствор насыщен кислородом до концентрации 5 × 10^–2 М, а равновесие в первой реакции устанавливается быстро, X^III – высокореакционноспособная частица.

1.5.33. (Пе1–2003, № 4). Реакция конверсии пара-водорода в орто-водород протекает по следующему механизму (M – инертная частица):

p-H₂ + M H ^· + H ^· + M,

H ^· + p-H₂ H ^· + о-H₂,

H ^· + H ^· + M p-H₂ + M.

Используя метод стационарных концентраций, получите выражение для скорости конверсии пара-водорода.

1.5.34. (КР1–2002, № 5). В системе присутствует вещество А с концентрацией А₀, которое может вступать в химические превращения по схеме

A 3 B,

2 B C,

где B – очень реакционноспособная частица.

Определите условие применимости метода квазистационарных концентраций. Найдите выражение для скорости образования С в момент времени, когда концентрация А равна концентрации С.

1.5.35. (КР1–2001, № 2). Для последовательной схемы превращения

2 A B C

известны значения констант скорости и энергии активации:

k1A0 = 2,8 × 10^–7 c^–1	k–1 = 3,3 × 10^–2 c^–1	k2 = 4,4 × 10^–3 c^–1
E1 = 40,0 ккал/моль,	E–1 = 33,0 ккал/моль,	E2 = 35,0 ккал/моль

Найдите энергию активации суммарного процесса 2 A ¾® С.

1.5.36. (Экз–2007, № 1). В закрытой системе проходят следующие реакции:

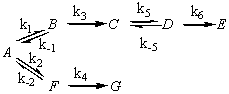
Найдите концентрации всех веществ после окончания реакций, если в начальный момент времени присутствует только вещество А c начальной концентрацией [A]₀ = a. Константы скорости отдельных стадий, выраженные в c^–1 равны: k₁ = 100; k_–1 = 200; k₂ = 300; k_–2 = 150; k₃ = 12; k₄ = 8; k₅ = 250; k_–5 = 190; k₆ = 320.

1.5.37. (КР1–2006, № 2). Разложение азотной кислоты в газовой фазе протекает по сложному механизму с образованием высоко-реакционноспособных промежуточных частиц ОН, NO и NO₃:

HNO₃ ¾® OH + NO₂ k₁

OH + NO₂ ¾® HNO₃ k₂

OH + HNO₃ ¾® H₂O + NO₃ k₃

NO₃ + NO₂ ¾® NO₂ + O₂ + NO k₄

NO₃ + NO ¾® 2 NO₂ k₅

Экспериментальная зависимость скорости образования кислорода при низких концентрациях NO₂ выражается формулой
W = a·[HNO₃], а при высоких – формулой W = b·[HNO₃]²[NO₂]^–1, где a и b – численные константы. Выразите k₁ и k₂/k₃ через а и b, используя приведённый механизм реакции.

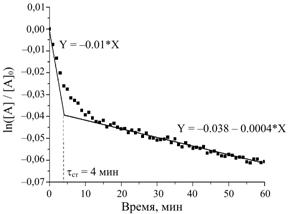
1.5.38. (КР1–2005, № 5). Для реакции, протекающей по схеме

A B C,

оцените константы скорости элементарных стадий k₁, k_–1 и k₂, используя представленную на следующем рисунке экспериментальную кинетическую кривую.

1.5.39. (КР1–2007, № 1). Окисление органического сульфида R₁SR₂ до сульфоксида может катализироваться комплексами титана Ti и TiL, где L – хиральный лиганд, причём TiL катализирует образование (R)-изомера сульфоксида, а Ti – образование рацемического сульфоксида:

Ti + L TiL (быстрое равновесие)

TiL + R₁SR₂ + H₂O₂ TiL + H₂O + сульфоксид-(R)

Ti + R₁SR₂ + H₂O₂ Ti + H₂O + сульфоксид-(рацемич. смесь).

В колбу поместили Ti и лиганд в равных концентрациях Ti₀ = L₀, добавили пероксид водорода и сульфид. Начальные концентрации комплекса и лиганда выбрали так, что K = 1/Ti₀ = 1/L₀. Найдите оптическую чистоту (С_R – C_S) / (C_R + C_S) образующегося сульфоксида, если k₁/k₂ = 10.

1.5.40. (КР1–2007, № 3). Разложение гидроперекиси кумола ROOH в присутствии ионов железа(II) происходит в соответствии со схемой

Fe^II + ROOH Fe^III + ,

,

C₂H₆.

Начальная квазистационарная скорость выделения газообразного этана из раствора объёмом 100 см³ составила 4,8 см³/с при 298 К и давлении 1 атм. Начальные концентрации ионов железа(II) 10^{–4 М и [}ROOH] = 1 M. Найдите k₁.

1.5.41. (КР1–2008, № 1).

Комплекс железа (V) Fe^V способен окислять алкен A в ацетонитриле в соответствии со схемой

Fe^V + A Fe^III + продукт

Fe^V + Fe^III Fe^IVFe^IV.

Обнаружено, что зависимость концентрации Fe^V от времени соответствует приведённому графику, если начальные концентрации Fe^V и A равны 0,05 М. Найдите значение k₁, если известно, что Fe^III – очень реакционноспособная частица, а димер Fe^IVFe^IV – инертное соединение.

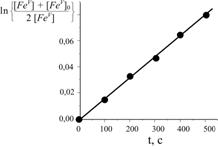
1.5.42. (КР1–2008, № 4). Гидролиз изоцианатов может протекать с промежуточным образованием карбаминовой кислоты по следующему механизму:

1) H₂O + R₃N X,

2) X + RNCO RNH–COOH + R₃N,

3) RNH–COOH + H₂O RNH₂ + H₂CO₃ (быстро).

Концентрации X и карбаминовой кислоты предполагаются квазистационарными. Получите выражение для начальной скорости реакции в квазистационарном приближении. Найдите эффективную энергию активации реакции при малых степенях превращения, полагая известными энергии активации всех стадий.

1.5.43. (КР1–1997, № 4). Образование АВ₂ происходит в результате реакций

1) A + B AB, 2) AB + B ¾® AB₂.

Оцените значение скорости реакции в момент, когда [A] уменьшится на 1/3, если k₁ = 10³ M^–1c^–1, k_–1 = 10⁴ c^–1, k₂ = 10⁶ M^–1c^–1, а начальные концентрации равны: [A]₀ = [B]₀ = 3 × 10^–3 М.