1. ФОРМАЛЬНАЯ КИНЕТИКА

1.6. Кинетика реакций в открытых системах

1.6.1. Необратимая реакция первого порядка A ¾® B происходит в реакторе идеального перемешивания, степень превращения равна 80 %. Среднее время пребывания реагента в реакторе равно t. Эту же реакцию проводят в реакторе идеального вытеснения, время пребывания реагента в реакторе также равно t. Чему равна степень превращения в реакторе идеального вытеснения?

Решите эту задачу принимая, что степень превращения в реакторе идеального перемешивания равна: 10 %, 20 %, 30 %, 40 %, 50 %, 60 %, 70 % и 90 %.

1.6.2. Для последовательной реакции

A B C

определите максимальную концентрацию промежуточного вещества [B]_max и необходимое для её достижения время контакта в реакторе идеального смешения, работающем в стационарном режиме. Сравните полученный результат с выражением для [B]_max для той же реакции в замкнутой системе.

1.6.3. (Пе1–2006, № 2). В реакторе идеального смешения проводится жидкофазная последовательная реакция

A B C.

Константы скорости равны: k₁ = 5 мин^–1, k₂ = 1,8 мин^–1. Объёмный расход Q смеси равен 300 л/мин, исходная концентрация вещества А равна 4,8 моль/л, исходные концентрации продуктов В и С равны нулю. Рассчитайте оптимальный объём реактора V_opt, позволяющий получить максимальное количество продукта В в стационарном режиме.

1.6.4. При какой объёмной скорости u_o подачи исходного компонента А в реактор идеального смешения можно ожидать в стационарных условиях получения наибольшего выхода продукта В, если этот продукт получается по схеме

2 A B P.

Объём реактора V, реагент A подаётся в большом избытке инертного разбавителя.

1.6.5. При какой объёмной скорости u_o подачи исходного компонента А в реактор идеального смешения можно ожидать в стационарных условиях получение наибольшего выхода продукта В, если этот продукт получается по схеме

A 2 B P.

Объём реактора V, реагент A подаётся в большом избытке инертного разбавителя.

1.6.6. При какой объёмной скорости u_o подачи исходного компонента А в реактор идеального смешения можно ожидать в стационарных условиях получение наибольшего выхода продукта В, если этот продукт получается по схеме

A B P

Объём реактора V. (Дополнительный вопрос: сопоставить решение с решением для реактора идеального вытеснения.)

1.6.7. При какой объёмной скорости u_o подачи исходного компонента А в реактор идеального смешения объёмом V можно ожидать в стационарных условиях получение наибольшего выхода продукта В, если этот продукт получается по схеме

A B C

1.6.8. В реакторе идеального смешения объёмом 0,1 л при постоянных Р и Т происходит мономолекулярная реакция разложения C₂H₅Cl на С₂Н₄ и HСl. При скорости подачи C₂H₅Cl 40 см³с^–1 степень его превращения в продукты равна 0,5. Какой будет степень превращения при увеличении скорости подачи вдвое?

Решить задачу для ситуаций, когда исходная смесь: 1) представляет собой чистый реагент; 2) сильно разбавлена инертным газом.

1.6.9. В идеально перемешиваемый растворитель объёма V, химически инертный по отношению к фенильному свободному радикалу, в течение длительного времени с постоянной скоростью W₀ вводится этот радикал, растворённый в том же растворителе. При этом общий объём v раствора, введённого за всё время эксперимента, удовлетворяет условию v << V. Введённый фенильный радикал рекомбинирует в получающемся более разбавленном растворе с константой скорости k₂, образуя дифенил.

Выведите уравнение, описывающее изменение концентрации фенильного радикала во времени, и найдите из него характеристическое время установления стационарной концентрации этого радикала. Начальную концентрацию радикала примите равной нулю.

1.6.10. В струевом реакторе длиной 80 см, диаметром 3,3 см при 520 °С и давлении 1 атм происходит разложение ацетальдегида в стационарных условиях по реакции

2 CH₃CHO ¾® 2 CH₄ + 2 CO.

Константа скорости этой реакции 0,33 М^–1×с^–1. Определите, какой процент ацетальдегида окажется разложившимся при скорости его подачи 50 г/ч.

1.6.11. В реакторе полного смешения объёмом 1 л при давлении 1 атм в стационарных условиях происходит реакция разложения

C₂H₅Br ¾® C₂H₄ + HBr.

Найдите область температур, при которых будет происходить 5 % и 50 % разложения бромистого этана, если скорость подачи 7 л/ч, а константа скорости k = 10¹³exp(–E/RT) с^–1, где E = 54 ккал/моль.

1.6.12. В реакторе идеального вытеснения при 450 °С и 1 атм происходит разложение метанола

CH₃OH CO + 2 H₂.

Найдите константу скорости реакции, если глубина пиролиза составляет 75 % при времени контакта t = 1,33 с.

1.6.13. В реактор полного смешения объёмом V подаётся со скоростью u_o смесь двух веществ с концентрациями [A]₀ и [B]₀. Между ними в реакторе идёт обратимая реакция

А В.

Найдите отношение концентраций [A]/[B] в стационарном режиме работы реактора. Сравните полученный результат с равновесными концентрациями А и В.

1.6.14. В проточный реактор поступает смесь СО (0,5 атм) и Н₂О:

CO + H₂O CO₂ + H₂.

Константа равновесия при температуре реактора равна K = 20, а константа скорости k₁ равна 10^–2 атм^–1 с^–1. Время нахождения смеси в реакторе 10² с. Рассчитайте степень превращения СО и Н₂О в СО₂ и Н₂ в процентах от максимально возможной, определяемой термодинамическим равновесием.

1.6.15. (Пе1–2003, № 5). Каталитическую реакцию паровой конверсии

СО + Н₂О ¾® Н₂ + СО₂

изучают в реакторе идеального вытеснения при давлении 20 атм, температуре 320 °С, загрузке катализатора 0,3 см³, объёмной скорости подачи исходной газовой смеси 0,6 л н.у./с и составе: СО – 17 об.%, Н₂О – 33 об.%, N₂ – 50 об.%. Установлено, что при этих условиях конверсия СО составляет 20 %, реакция является практически необратимой, характеризуется первым порядком по концентрации СО и нулевым порядком по концентрации Н₂О. Определите эффективную константу скорости реакции.

1.6.16. (Пе1–2008, № 2). В реактор идеального перемешивания подаётся эквимолекулярная смесь 50 % МеОН + 50 % азота. В реакторе происходит реакция разложения метанола с образованием СО и водорода. Порядок реакции по метанолу – первый. Температура 400 °С, давление 1 атм, скорость подачи азотно-метанольной смеси u = 1 л/с, объём реактора V = 1 литр, константа скорости k = 1 с^–1. Найдите степень превращения метанола.

1.6.17. В реакторе периодического действия должна быть достигнута производительность 50 т/сутки по этилацетату, получаемому из этилового спирта и уксусной кислоты:

C₂H₅OH + CH₃COOH CH₃COOС₂H₅ + H₂O.

(А) (В) (R) (S)

Скорость реакции в жидкой фазе

.

При 100 °С k = 7,93 × 10^–6 м³/(кмоль×с), K = 2,93, в исходной жидкости содержится 23 вес.% кислоты, 16 вес.% спирта и отсутствует эфир. Должна достигаться степень превращения кислоты – 35 %. Плотность жидкости примерно постоянна и равна 1080 кг/м³. Реактор будет работать 24 часа в сутки. Время для заполнения, опустошения и пр. составляет в сумме для подобных реакторов 1 ч. Какой требуется объём реактора?

1.6.18. (Экз–2006, № 1). В реакторе полного смешения протекает мономолекулярная необратимая реакция:

A B, k = 10^–2 c^–1.

Время контакта реакционной смеси t = 50 с. Первоначально в реактор подают сильно разбавленный инертным газом реагент А с начальной концентрацией 10^–3 М до установления стационарной концентрации, а затем концентрацию А в подаваемой смеси скачком уменьшают до нуля. Найдите концентрации А и B в реакторе через 100 c после скачкообразного изменения начальной концентрации реагента А.

1.6.19. (КР1–2002, № 4). Реагент B с объёмной скоростью 1 см³/с подаётся в реактор полного смешения объёмом 1 см³. В реакторе происходит реакция B ® P, константа скорости равна 2 с^–1. Концентрация B₀ на входе в реактор изменяется во времени следующим образом:

, b = 0,01 моль/л×с.

Определите концентрацию на выходе из реактора в моменты времени t и 2 t, если t = 1/3 с.

1.6.20. Димеризация изопрена (растворённого в большом количестве инертного разбавителя) изучалась в струевом реакторе идеального вытеснения объёмом 1 л при постоянной скорости струи 10 см³/с. При парциальном давлении изопрена P = 0,1 мм рт. ст. и разных температурах состав продуктов оказался следующим.

T, K	550	600	650	700	750
C10H16/C5H8	3 × 10^–5	2,4 × 10^–4	1,5 × 10^–3	6,6 × 10^–3	2,4 × 10^–2

Определите по этим данным предэкспоненциальный множитель и энергию активации константы скорости этой реакции.

1.6.21. (КР1–1997, № 3). Стехиометрическая смесь CO и N₂O пропускается через реактор идеального вытеснения со скоростью 5 см×с^–1. Начальные концентрации CO и N₂O равны 10^–3 М, а константа скорости реакции равна 0,46 М^–1с^–1.

При какой длине реактора концентрации всех компонентов (CO, CO₂, N₂O и N₂) на выходе реактора будут одинаковыми?

1.6.22. (КР1–1998, № 4). В реакторе идеального смешения объёмом 0,1 л вещество А необратимо изомеризуется в вещество В с константой скорости 1 × 10^–2 с^–1. На вход реактора подаётся вещество А с начальной концентрацией 0,2 М. Объёмные скорости ввода и вывода рабочих растворов равны 1 см³с^–1. Оцените концентрации веществ А и В по прошествии 6 мин с момента запуска процесса.

1.6.23. (КР1–2001, № 3). В реакторе полного перемешивания протекают превращения согласно схеме

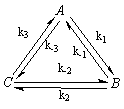
Раствор реагента А с концентрацией 1 М подаётся в реактор с объёмной скоростью 10 см³/с, объём реактора 5 см³; k_–1 = 2 c^–1, k₂ = 5 c^–1, k_–2 = 4 c^–1, k₃ = 10 c^–1.

Покажите, что k₁k₂k₃ / k_–1k_–2k_–3 = 1, и определите k₁ и k_–3, если известно, что отношение концентраций B/A на выходе равно 0,5. Реактор работает в стационарном режиме.

1.6.24. (КР1–2003, № 3). В реактор полного смешения объёмом 1,0 л при температуре 520 °С и давлении 1 атм подаётся чистый ацетальдегид с объёмной скоростью 20 мл/с. В реакторе происходит необратимая мономолекулярная реакция разложения ацетальдегида на метан и СО

CH₃CHO ¾® CH₄ + CO

с константой скорости k = 2 × 10^–2 c^–1. Найдите концентрацию ацетальдегида на выходе из реактора, предполагая, что реактор работает в стационарном режиме.

1.6.25. (КР1–2003, № 4). Реактор идеального вытеснения состоит из двух одинаковых ступеней, между которыми имеется теплообменник. Температура первой ступени 200 °С, температура второй ступени 180 °С.

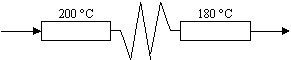
В реакторах идёт реакция изомеризации вещества A ¾® B. Степень превращения после первой ступени равна 50 %. Чему равна степень превращения на выходе из реактора, если время контакта одинаково для первой и второй ступеней, а энергия активации этой реакции равна 100 кДж/моль.

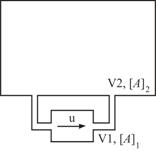
1.6.26. (Экз–2004, № 1). Два реактора полного перемешивания объёмом V1 и V2 литров соединены так, как показано на рисунке. В реакторе 1 протекает мономолекулярная реакция превращения газа А в газ B с константой скорости k. Температуры реакторов одинаковы. Найдите зависимость концентрации А от времени для каждого из реакторов, если в начальный момент [A]₁ = [A]₂ = a. Объёмом соединительных линий пренебречь.

1.6.1. (КР1–2005, № 2). Получение продукта P из реагента A проходит в 2 стадии. На первой стадии чистый газообразный A подаётся в реактор полного смешения, в котором происходит реакция (1). Объём реактора 1 л, скорость подачи 0,1 л/с, степень превращения 0,95.

Получившаяся смесь сразу же подаётся на вход реактора идеального вытеснения (объём 1 л), в котором идёт реакция (2).

2)

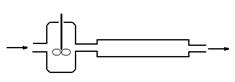
Известно, что k₂ = 0,1 × k₁. Определите селективность процесса по продукту Р (отношение количества образовавшегося продукта P к количеству израсходованного реагента А).

1.6.2. (КР1–2006, № 3). Реакцию дегидратации изопропанола

C₃H₇OH ¾® C₃H₆ + H₂O

проводили в реакторе идеального вытеснения при постоянном давлении 1 атм. Установлено, что порядок реакции по изопропанолу равен единице. Если в исходной смеси изопропанол сильно разбавлен инертным газом, то степень превращения x равна 0,8 при температуре 200 °С. Объёмная скорость подачи исходной реакционной смеси 0,2 мл/с, объём реактора 1 мл.

Чему будет равна степень превращения изопропанола, если в реактор подавать чистый газообразный изопропанол с такой же объёмной скоростью?

1.6.3. (КР1–2007, № 5). На вход реактора идеального вытеснения объёмом 250 см³ подаётся реагент A при атмосферном давлении и температуре 298 K с начальной объёмной скоростью потока 10 см³/с. В реакторе происходит процесс

3 A B.

Найдите величину константы скорости k, если известно, что на выходе из реактора скорость потока уменьшается вдвое по сравнению с начальной.

Решите предыдущую задачу, считая что реакция происходит в реакторе полного перемешивания.

(КР1–2008, № 2). Селективная тетрамеризация этилена в 1-октен проводится в стационарных условиях в реакторе полного перемешивания (в реактор подаётся газообразный этилен, в результате реакции образуется жидкий октен). При малых временах контакта t₀ степень превращения этилена a линейно зависит от времени контакта

,

причём коэффициент пропорциональности b не зависит от давления в реакторе. Определите порядок реакции по этилену.

1.6.4. (Экз–2007, № 5). В реакторе полного смешения при атмосферном давлении протекает метанирование смеси СО и СО₂:

1) ,

2) .

Начальные концентрации реагентов равны: 10 об.% СО, 30 об.% СО₂, 60 об.% Н₂, метан и вода отсутствуют.

Найдите концентрации всех веществ на выходе из реактора, если степени превращения СО и СО₂ составляют 0,8 и 0,167 соответственно.

1.6.33. В реакторе идеального вытеснения происходит сложная реакция

A + B D

D P.

На вход реактора объёма V = 250 мл c объёмной скоростью u₀ = 50 мл/мин подаётся реакционная смесь, содержащая реагенты А и В в концентрациях С_А⁰ = 0,01 М, С_В⁰ = 0,1 М, k₁ = 0,1 М^–1с^–1 , k_–1 = 1,5 с^–1, k₂ = 2 с^–1. Найдите степень превращения А на выходе реактора.

1.6.34. В реакторе идеального вытеснения происходит реакция

A + B 3 C.

На вход реактора объёма V c объёмной скоростью u₀ подаётся реакционная смесь, содержащая чистые реагенты А и В в равных концентрациях С_А⁰ = С_В⁰ = а. Найдите зависимость степени превращения реагентов А и В от объёмной скорости подачи реагентов.

1.6.35. В реакторе идеального вытеснения происходит реакция

A 2 C

На вход реактора объёма V c объёмной скоростью u₀ подаётся реакционная смесь, содержащая чистый реагент А в концентрации С_А⁰. Найдите зависимость степени превращения реагента от объёмной скорости подачи.