2. АБСОЛЮТНЫЕ ЗНАЧЕНИЯ СКОРОСТЕЙ ХИМИЧЕСКИХ РЕАКЦИЙ

2.2. Теория переходного состояния

Расчет константы скорости

2.2.1. Сформулируйте основные предположения, на которых базируется теория активированного комплекса. Выведите основную формулу теории активированного комплекса, выражающую константу скорости реакции через статистические суммы активированного комплекса и реагентов и критическую энергию Е₀.

2.2.2. Выведите выражение для константы скорости произвольной элементарной реакции в рамках термодинамической формулировки теории активированного комплекса.

2.2.3. Докажите, что для бимолекулярной реакции между атомами теория столкновений и теория активированного комплекса дают одинаковые формулы для предэкспоненциального множителя константы скорости.

2.2.4. Выведите выражение для константы скорости бимолекулярной реакции атома с двухатомной молекулой

А + ВС ¾® АВ + С,

используя теорию активированного комплекса.

2.2.5. Оцените по порядку величины стерический фактор для реакции, идущей через линейный активированный комплекс, между двумя линейными молекулами.

2.2.6. На основе метода активированного комплекса определите вид температурной зависимости предэкспонента в бимолекулярной реакции атома с двухатомной молекулой (треугольный и линейный активированные комплексы). Колебательные степени свободы не учитывать.

2.2.7. Опираясь на представления теории активированного комплекса, получите выражение для оценки стерического фактора для реакции между тремя двухатомными молекулами. Активированный комплекс считать нелинейным.

2.2.8. Методом активированного комплекса дайте сравнительную оценку стерических множителей двух каналов следующей элементарной бимолекулярной реакции:

2.2.9. Методом активированного комплекса оцените отношение предэкспоненциальных множителей двух элементарных реакций

H₂ + F₂ ¾® 2 HF,

H₂ + F₂ ¾® H + HF + F.

2.2.10. Пользуясь теорией активированного комплекса, оцените по порядку величины стерический фактор и предэкспонент для реакции

О + СО ¾® СО₂.

2.2.11. (КР2–2004, № 1). Определите температурную зависимость константы скорости простой тримолекулярной реакции

2 NO + Cl₂ = 2 NOCl

при температурах, близких к комнатной. Найдите связь между истинной и наблюдаемой (аррениусовской) энергиями активации в предположении нелинейного активированного комплекса.

2.2.12. (КР2–2001, № 3). Рассчитайте предэкспоненциальный множитель для реакции обмена при Т = 1000 К, протекающей через линейный активированный комплекс

.

В молекуле частота валентных колебаний n_H–H = 4396 см^–1, длина связи R_H–H = 0,74 Å. В активированном комплексе R_H–H = 0,92 Å, частота дважды вырожденного деформационного колебания равна 900 см^–1, симметричного – 2100 см^–1.

2.2.13. (КР2–2002, № 3). По методу активированного комплекса проведите расчёт предэкспонента в реакции

H–CºC–H .

Активированный комплекс считать линейным. При расчёте принять, что межатомные расстояния C–H в молекуле ацетилена равны 1,06 Å; СºС в молекуле ацетилена и все расстояния в активированном комплексе – 1,2 Å. Колебательными статсуммами пренебречь. Температура 500 К.

2.2.14. Оцените стерический фактор и предположите характер температурной зависимости предэкспоненциального множителя константы скорости реакции

H–CºC–H .

2.2.15. На основании теории абсолютных скоростей реакции оцените стерический фактор для тримолекулярного процесса

2 NO + O₂ ¾® 2 NO₂.

2.2.16. Пользуясь теорией активированного комплекса, оцените по порядку величины стерический фактор и предэкспонент для следующей реакции:

Разрешена ли эта реакция по правилу Вудворда – Гоффмана?

2.2.17. Методом активированного комплекса рассчитайте константу равновесия процесса

H₂ + D₂ 2 HD

при высоких температурах.

2.2.18. Оцените предэкспоненциальный фактор константы скорости реакции Br + H₂ ¾® HBr + H при 200 К. Активированный комплекс считать линейным. Длина связи Н–Н в активированном комплексе равна 1,5 Å, а в молекуле Н₂ » 0,74 Å. Длина связи Н–Br в активированном комплексе 1,4 Å. Колебания в активированном комплексе двух типов: n_s – валентные и n_j – деформационные, последние дважды вырождены; n_s = 2340 см^–1, n_j = 460 см^–1. Частота колебаний атомов в молекуле водорода n = 4396,5 см^–1.

2.2.19. (КР2–2003, № 3). В таблице приведены параметры переходного комплекса для реакции SiF₃H + H ® SiF₃ + H₂.

	Частота колебаний, cм^–1	Энергия, ккал/моль
SiF3H	307, 307, 422, 854, 879, 1015, 1015, 2463	–20
¹	184, 184, 302, 302, 406, 836, 970, 970, 1108, 1108, 1248	–10

Оцените константу скорости реакции при 300 К предполагая, что моменты инерции, а также массы переходного комплекса и трифторсилана примерно равны. При расчёте колебательных статсумм учитывать только колебания с q/Т < 3.

2.2.20. (КР2–2006, № 4). Оцените константу скорости реакции пиролиза йодистого метила при 600 К

CH₃I СН₃ + I,

если , волновые числа дважды вырожденного деформационного колебания в реагенте и переходном комплексе n_d = 1150 и = 230 см^–1, истинная энергия активации Е_а+ = 240 кДж/моль. Волновое число валентного колебания С–I в йодметане n_C–I = 500 см^–1, а частоты других колебаний при реакции изменяются незначительно. Чему равна константа скорости обратной реакции

СН₃ + I CH₃I,

если её термодинамические параметры = –120 Дж/(моль×К), = –240 кДж/моль (P₀ = 1 атм)?

2.2.1. Константа равновесия обратимой реакции

C₂H₄ + HBr C₂H₅Br

c тепловым эффектом DН = –17 ккал/моль равна 0,006 л/моль при 255 °С. Оцените стерический фактор прямой реакции. Сопоставьте полученную величину с оценкой по методу активированного комплекса, полагая, что колебательные степени свободы при этой температуре не возбуждены, а средний момент инерции молекул C₂H₄, HBr и активированного комплекса при этой температуре равен 10^–39 г×см². Диаметр молекул принять: C₂H₄ = 5,3 Å, HBr = 3,1 Å.

2.2.2. По методу активированного комплекса провести расчёт предэкспоненциального множителя в реакции

,

считая комплекс пирамидой, в основании которой лежат молекулы кислорода на расстоянии 2 Å друг от друга, а в вершине (h = 2 Å) – атом Н. Расстояние O–O в молекуле кислорода равно 1,2 Å, T = 500 К.

2.2.3. Рассчитайте при 500 К предэкспоненциальный множитель и стерический фактор для реакции

.

Колебательными статистическими суммами пренебречь. Длины связей С–С и С–Н в бензоле и активированном комплексе принять равными 1,4 и 1,1 Å, газокинетические радиусы хлора и бензола 2,0 и 3,0 Å. Конфигурацию активированного комплекса принять в виде пирамиды с высотой h = 3,2 Å, в основании которой лежит молекула бензола, а в вершине – атом хлора.

2.2.4. (КР2–2007, № 3). Рассчитайте по теории активированного комплекса константу скорости при 300 К для простой бимолекулярной реакции

^,

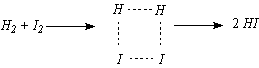если предположить, что:

a) активированный комплекс имеет плоское строение, три главных момента инерции равны соответственно: I_A = 920 · 10^–47 кг·м², I_B = 10 · 10^–47 кг·м², I_C = 930 · 10^–47 кг·м²;

б) для молекул исходных веществ расстояния H–H и I–I равны 0,074 нм и 0,25 нм, атомная масса йода 127 г/моль, атомная масса водорода 1 г/моль;

в) все колебательные степени свободы заморожены;

г) истинная энергия активации 167,36 кДж/моль.

2.2.5. Проведите расчёт отношения величин предэкспоненциальных множителей для констант скорости реакций атомов галоидов Х = Cl, Br с молекулой Н₂, идущих при 1000 К:

.

Активированный комплекс считать линейным с расстояниями = 1,5 Å и = 1,4 Å. Колебания в активированном комплексе двух типов: n_S – валентные и n_j – деформационные; последние дважды вырождены:

H–H–Cl, n_S = 2496 см^–1, n_j = 551 см^–1,

H–H–Вr, n_S = 2340 см^–1, n_j = 460 см^–1.

2.2.6. Проведите расчёт предэкспоненциального множителя k₀ для константы скорости реакции

считая активированный комплекс линейным по связям .

Метильный радикал считать плоским с параметрами R_C–H = 1,1 Å, ÐHCH = 120°. Другие геометрические параметры: = 1,4 Å, R_H–H = 0,74 Å (в молекуле Н₂ и комплексе), Т = 400 К.

2.2.7. Для реакции рассчитайте k₀ методом активированного комплекса, предполагая, что комплекс линейный с расстояниями между атомами 0,92 Å, а вклад в k₀ за счёт трансмиссионного коэффициента и колебательных статистических сумм равен 1,5 × 10³. Температура 500 К.

2.2.8. Установлено, что для реакции атома с двухатомной молекулой аррениусовская (наблюдаемая) энергия активации совпадает с истинной энергией активации. Определите в рамках теории активированного комплекса строение активированного комплекса (линейный или треугольный) и оцените стерический фактор этой реакции.

2.2.9. Найдите истинную энергию активации реакции диспропорционирования

,

протекающей в газовой фазе через линейный переходный комплекс, если эффективная энергия активации составляет 10,5 кДж/моль.

2.2.10. (Пе2–2006, № 3). Рассчитайте по приведенной на рисунке поверхности потенциальной энергии для реакции I + HgI ¾® IHg + I константу скорости при Т = 300 °С. Колебательными статсуммами пренебречь, активированный комплекс считать линейным. Высота активационного барьера 800 см^–1, M_Hg = 200,6 г/моль, M_I = 126,9 г/моль.

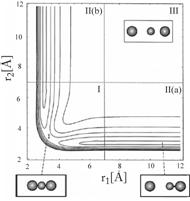
2.2.11. (КР2–2008, № 1). Вычислите значение стерического фактора для бимолекулярной реакции

2 NOCl ¾® 2 NO + Cl₂,

если газокинетический радиус NOCl составляет 2 нм, а предэкспоненциальный множитель зависит от температуры следующим образом: = 7,71.

2.2.12. (КР2–2008, № 2). Вычислите константу скорости реакции

O + CO ¾® [O···C···O] ^≠ ¾® CO₂

при 1000 К на основании следующих данных:

а) активированный комплекс имеет линейное строение. Межъядерное расстояние C×××O в активированном комплексе составляет 1,2 · 10^‑10 м, частота дважды вырожденных деформационных колебаний n = 6 · 10¹² с^–1, вырождение основного электронного состояния g₀ = 1, симметричное колебание заморожено;

б) в молекуле СО межъядерное расстояние равно 1,12 · 10^–10 м, вырождение основного электронного состояния g₀ = 1, колебательная степень свободы заморожена;

в) для атома кислорода вырождение основного электронного состояния g₀ = 5;

г) истинная энергия активации составляет 83,68 кДж/моль;

д) трансмиссионный коэффициент равен 1.

2.2.13. (КР2–2008, № 3). В газовой фазе протекает простая бимолекулярная реакция

О⁺ + N₂ ¾® [O···N···N]⁺ → ON⁺ + N.

Активированный комплекс имеет линейное строение, истинная энергия активации реакции равна нулю. Зная, что константа скорости реакции достигает минимума при температуре 500 °С, вычислите волновое число (см^–1) дважды вырожденных деформационных колебаний активированного комплекса. Остальные колебательные степени свободы активированного комплекса и N₂ можно считать замороженными.

2.2.14. (КР2–2008, № 5). Используя вариационную теорию активированного комплекса, оцените расстояние между ионами в активированном комплексе [Cs⁺ ··I^–]^¹ при распаде этой молекулы в газовой фазе. При расчёте принять, что взаимодействие между ионами описывается кулоновским потенциалом, T = 2000 К.