2. АБСОЛЮТНЫЕ ЗНАЧЕНИЯ СКОРОСТЕЙ ХИМИЧЕСКИХ РЕАКЦИЙ

2.3. Изотопные эффекты

2.3.1. Реакция нитрирования ароматических углеводородов описывается схемой

ArONO₂ ArO^– + NO₂⁺,

NO₂⁺ + ArH ArNO₂ + H⁺.

В параллельных опытах было показано, что скорости нитрирования бензола и гексадейтеробензола при равных начальных концентрациях реагентов одинаковы и описываются уравнением

W = k_Н ×[ArONO₂].

Однако в опыте с одновременным присутствием равных количеств бензола и гексадейтеробензола скорости их расходования различны. Скорость расходования бензола в четыре раза выше, чем скорость расходования гексадейтеробензола. Объясните эти результаты.

2.3.2. Используя теорию активированного комплекса, выведите формулу, описывающую кинетический изотопный эффект для реакции между органической молекулой R–H и радикалом :

,

,

при условии, что массы свободных радикалов и и атома удовлетворяют условиям , .

Оцените кинетический изотопный эффект при 300 К, считая, что частота валентного колебания связи R–H равняется 3000 см^–1, а вкладом других колебаний можно пренебречь.

2.3.3. Оцените вклады поступательных, вращательных и колебательных степеней свободы в кинетический изотопный эффект для реакции

+ C₃ H₈ ¾® H₂ + H₇,

+ C₃ H₈ ¾® HD + H₇

и величину суммарного изотопного эффекта при температуре 300 К. При расчёте необходимо учесть дважды вырожденные деформационные колебания атакующего атома в переходных комплексах с частотами = 400 см^–1 и = 350 см^–1.

2.3.4. Оцените вклады поступательных, вращательных и колебательных степеней свободы в кинетический изотопный эффект для реакции

,

и величину суммарного изотопного эффекта при температуре 300 К. При расчёте необходимо учесть дважды вырожденные деформационные колебания атакующего атома в переходных комплексах с частотами = 400 см^–1 и = 350 см^–1.

Оцените вклады поступательных, вращательных и колебательных степеней свободы в кинетический изотопный эффект для реакции

,

и величину суммарного изотопного эффекта при температуре 300 К. При расчёте необходимо учесть дважды вырожденные деформационные колебания атакующего атома в переходных комплексах с частотами = 400 см^–1 и = 350 см^–1.

2.3.4п. Методом активированного комплекса рассчитайте отношение предэкспоненциальных множителей реакции

Cl + H₂ ¾® HСl + H,

Cl + D₂ ¾® DСl + D,

считая активированный комплекс линейным с длинами связей  Å,  Å. Расчёт проведите при температурах, когда колебательные статистические суммы исходных молекул и активированных комплексов можно считать равными единице.

2.3.5. Пользуясь теорией активированного комплекса, оцените стерический фактор реакции

D + I₂ ¾® DI + I ,

протекающей через линейный активированный комплекс, и величину изотопного эффекта при замене D на H. Температура 300 К. Частота дважды вырожденных деформационных колебаний в комплексе составляет = 400 см^–1, = 280 см^–1.

2.3.6. Вычислите вклад поступательных степеней свободы в кинетический изотопный эффект для реакций отрыва атома от молекулы углеводорода RH атомами и .

2.3.7. Рассчитайте изотопный эффект в реакциях

СH₄ + ¾® + HCl,

СD₄ + ¾® + DCl

при 500 К для линейного активированного комплекса

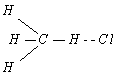
при длине связи С–Н, равной 1,1 Å; H–Cl, равной 1,3 Å. В колебательной статистической сумме учесть только 4 колебания активированного комплекса, приняв . Для молекулы метана n_CH = 3000 см^–1.

2.3.8. (КР2–2004, № 4). Оцените отношение констант скорости при 200 К для реакции

,

,

учитывая, что частота валентного колебания С–Н в молекуле метана равна 3000 см^–1. При решении пренебречь вкладом изотопного эффекта в поступательные степени свободы и изменением момента инерции переходного комплекса.

Реакция протекает через трехцентровый активированный комплекс, причём атомы C–H–Cl лежат на одной прямой, а положения атомов водорода в метильной группе эквивалентны:

^.

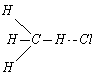2.3.9. (КР2–2003, № 2). Оцените кинетический изотопный эффект для распада хлороформа и тритохлороформа (отщепление изотопа водорода) при 500 К. Волновое число валентного колебания С–Н в хлороформе 3032 см^–1, вкладом деформационных колебаний пренебречь.

2.3.10. (КР2–2000, № 4). Оцените величину кинетического изотопного эффекта для реакции

CH₂DCOOH + CH₃COO ¾® CH₂COOH + CH₃COOD, k_D

CH₂DCOOH + CH₃COO ¾® CHDCOOH + CH₃COOH, k_H

при температуре 298 К, если частота валентного колебания C–H составляет 3000 см^–1 (деформационные колебания не учитывать).

2.3.11. (КР2–2002, № 2). Оцените отношение констант скоростей для реакции

,

.

Атомы D и H находятся в пара-положении, w_С–H = 3050 см^–1, Т = 300 К. Деформационные колебания не учитывать.

2.3.12. Оцените вклад поступательных, вращательных и колебательных степеней свободы в кинетический изотопный эффект для реакции

H₂ + R ¾® H + HR,

HD + R ¾® D + HR.

Считать, что >>, w_H–H = 4396,5 см^–1. В переходном комплексе имеются дважды вырожденные деформационные колебания = 400 см^–1, = 280 см^–1. Т = 300 К.

2.3.13. (КР2–2007, № 5). Оцените кинетический изотопный эффект при 500 К в реакциях

1) SiH₄ + I ¾® SiH₃ + HI,

2) SiD₄ + I ¾® SiD₃ + DI.

Молекула силана имеет тетраэдрическое строение, частота валентного колебания в силане n_SiH = 2190 см^–1. Изменение частот других колебаний в активированном комплексе не учитывать. Активированные комплексы имеют ось симметрии третьего порядка Si×××(H)×××I, M_Si = 28 г/моль.

2.3.14. (КР2–2008, № 4). Рассчитайте кинетический изотопный эффект при 300 К для реакции

H + H₂ [ H···H···H ]^≠ ¾® H₂ + H

D + H₂ [ D···H···H ]^≠ ¾® HD + H,

если известно, что в активированном комплексе частота деформационных колебаний в обоих случаях близка, а волновые числа симметричных валентных колебаний n_H и n_D равны 2012 и 1732 см^–1 соответственно. Активированный комплекс имеет линейное строение с одинаковыми расстояниями R_H–H и R_D–H.

2.3.15. (Экз–2006, № 4). Оцените кинетический изотопный эффект для реакции образования нитрометильного катиона в водном растворе при температуре 298 К, :

CH₃NO₂ + OH^– ¾®

CD₃NO₂ + OH^– ¾® .